A) 89.28cm
B) 200 cm
C) 250 cm
D) 312.5 cm
Correct Answer: A
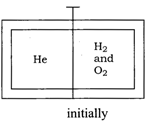
Solution :
Idea This question can be solved by using the concept of stoichiometry and volume-mole relationship. \[{{H}_{2}}+\frac{1}{2}{{O}_{2}}\xrightarrow[{}]{{}}{{H}_{2}}O\] Since mole of \[{{H}_{2}}\] reacts with \[\frac{1}{2}\] moles of \[{{O}_{2}}\]. Hence, net chemical reaction occuring at compartment and moles of \[{{O}_{2}}\] remain after reaction is\[2{{H}_{2}}+{{100}_{2}}\xrightarrow[{}]{{}}\underset{\begin{smallmatrix} \text{Volume}\,\text{of}\,{{H}_{2}}O \\ \text{will}\,\text{not}\,\text{considered} \end{smallmatrix}}{\mathop{\underset{\downarrow }{\mathop{2{{H}_{2}}O+9{{O}_{2}}}}\,}}\,\] After reaction Moles of He in compartment = 5 Moles of \[{{O}_{2}}\] in compartment = 9 Total moles of \[{{H}_{2}}\] and \[{{O}_{2}}\]after reaction = 9+ 5 =14 Since, volume of gases \[\propto \] number of moles of gases due to same temperature and pressure. Length of the compartment \[=\frac{\text{moles}\,\text{of}\,\text{He}}{\text{Total}\,\text{mole}}\times \] length of full compartment\[=\frac{5}{5+9}\times 250\] \[=\frac{1250}{14}=89.28\,\text{cm}\] TEST Edge Students are advised to undergo the concept of ideal gas and van der Waal's gas equation also to solve the problem of various kind including conceptual mixing of mole concept and ideal gas which are asked very frequently.You need to login to perform this action.
You will be redirected in
3 sec
