question_answer

A uniform metal disc of radius R is taken and out of it a disc of diameter R/2 is cut-off from the end. The centre of mass of the remaining part will be

A)  \[\frac{R}{4}\]from the centre    

B)  \[\frac{R}{3}\]from the centre      

C)  \[\frac{R}{5}\]from the centre    

D)  \[\frac{R}{6}\]from the centre

Correct Answer: D

Solution :

 Idea Here, disc could be considered as the combination of two parts as shown in the figure. The centre of mass of the combination (complete disc) is at O. If we consider origin and centre of mass at the same point, then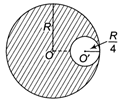 \[{{M}_{1}}\]and\[{{M}_{2}}\]are the masses of the two parts. Mass of the disc removed \[=\frac{M}{\pi {{R}^{2}}}\times \pi {{\left\{ \frac{R}{2} \right\}}^{2}}=\frac{M}{4}\] Remaining mass\[=M-\frac{M}{4}=\frac{3M}{4}\] Let, the origin of the coordinate system coincide with centre of mass of whole disc. Now, we know that \[{{X}_{CM}}=\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}\] \[{{X}_{CM}}\]will be zero, when\[{{m}_{2}}{{x}_{2}}=-{{m}_{1}}{{x}_{1}}\] \[\therefore \]\[{{x}_{2}}=\frac{{{m}_{1}}}{{{m}_{2}}}{{x}_{1}}\] Here, \[{{m}_{1}}=\frac{M}{4},{{x}_{1}}=\frac{R}{2}\] and \[{{m}_{2}}=\frac{3M}{4}\] (For remaining mass) Hence, \[{{x}_{2}}=-\frac{M/4}{3M/4}.\frac{R}{2}=\frac{-R}{6}\] i.e., \[\frac{R}{6}\]from the centre (on LHS). TEST Edge If a body is in rolling motion, the velocity of centre of mass gives translational velocity of the body. If we sit on the centre of mass, the rotational part of the rolling motion could be understood.