question_answer

The range of \['\alpha '\] for which the point \[(\alpha ,\alpha )\] lies inside the region bounded by the Curves \[y=\sqrt{1-{{x}^{2}}}\]and \[x+y=1\] is -

A) \[\frac{1}{2}<\alpha <\frac{1}{\sqrt{2}}\]

B) \[-\frac{1}{\sqrt{2}}<\alpha <\frac{1}{\sqrt{2}}\]

C) \[\alpha >\frac{1}{\sqrt{2}}\]

D) \[0<\alpha <\frac{1}{2}\]

Correct Answer: A

Solution :

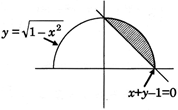\[\Rightarrow 2{{\alpha }^{2}}-1<0\]\[\Rightarrow -\frac{1}{\sqrt{2}}<\alpha <\frac{1}{2}\]        ??..(1)

and \[\alpha +\alpha >1\]           \[\Rightarrow \alpha >\frac{1}{2}\]                ???(2)

\[\therefore \]Common solution of (1) and (2) is:

\[\frac{1}{2}<\alpha <\frac{1}{\sqrt{2}}\]