question_answer

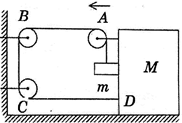
In figure shown, find the magnitude of acceleration of m, given that string is inextensible and mass less and the acceleration of M is \[2\text{ }m/{{s}^{2}}\] towards left -

A) \[2\sqrt{3}\,\,m/{{s}^{2}}\]

B) \[3\sqrt{2}\,\,m/{{s}^{2}}\]

C) \[4\sqrt{2}\,\,m/{{s}^{2}}\]

D) \[2\sqrt{5}\,\,m/{{s}^{2}}\]

Correct Answer: D

Solution :

Let X be the leftward displacement of m and x and y be the leftward and downward displacement of M.

Let \[AB={{\ell }_{1}};\] \[BC={{\ell }_{2}}:\] \[CD={{\ell }_{3}}\] and \[Am={{\ell }_{4}}\]when M moves towards left, say by x, then

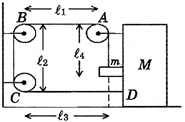\[AB=({{\ell }_{1}}-x)\]

\[BC={{\ell }_{2}}\]

\[CD={{\ell }_{3}}-x\]

\[Am={{\ell }_{4}}+y\]

Total length of string remain constant

\[\therefore {{\ell }_{1}}-x+{{\ell }_{2}}+{{\ell }_{3}}-x+{{\ell }_{4}}+y={{\ell }_{1}}+{{\ell }_{2}}+{{\ell }_{3}}+{{\ell }_{4}}\]

\[\therefore 2x=y\]

Acceleration of \[M={{a}_{M}}=2m/{{s}^{2}}\]

\[{{a}_{x}}=2m/{{s}^{2}}\]

\[2x=y\]

Double differentiating this equation

\[2{{a}_{x}}={{a}_{y}}\]

\[{{a}_{y}}=2{{a}_{x}}=4m/{{s}^{2}}\]

\[{{a}_{y}}\] is downward acceleration of \[m=4m/{{s}^{2}}\]

m is also moving in left direction along with M.

m has acceleration in horizontal direction also horizontal acceleration of m is same as that of M i.e. \[2\,m/{{s}^{2}}\]

\[\therefore \] Net acceleration of \[m=\sqrt{{{2}^{2}}+{{4}^{2}}}=2\sqrt{5}\]