| A block of mass m is pushed across a rough surface by an applied force F, directed at an angle \[\theta \] relative to the horizontal as shown. The block experiences a friction force \[f\] in the opposite direction. What is the coefficient of friction between the block and the surface? |
 |
A) \[\frac{mg}{F\,\,\sin \phi }\]
B) \[\frac{f}{F\,\,\sin \phi +mg}\]
C) \[\frac{f}{mg}\]
D) \[\frac{mg}{f}\]
Correct Answer: B
Solution :
| the key to finding the coefficient of friction \[\mu \]is in calculating the correct normal force acting on the block |
| \[\sum{Fy=m{{a}_{y}}}\] |
| Free body diagram |
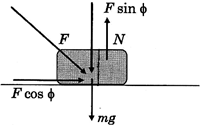 |
| Block does not move in y direction |
| \[\therefore {{a}_{y}}=0\] |
| \[\therefore N=F\sin \phi +mg\] |
| \[\mu =\frac{{{F}_{friction}}}{N}=\frac{f}{F\sin \phi +mg}\] |
You need to login to perform this action.
You will be redirected in
3 sec
