question_answer

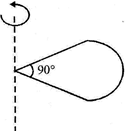
One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is

A) \[\frac{1}{2}M{{R}^{2}}\]

B) \[\frac{1}{4}M{{R}^{2}}\]

C) \[\frac{1}{8}M{{R}^{2}}\]

D) \[\sqrt{2}M{{R}^{2}}\]

Correct Answer: A

Solution :

We cannot consider the quadrant as a single mass as the distance of different particles is different from the axis of rotation. So, we take the help of calculus. Let us consider a segment as shown in the figure. All masses lying in this segment are at a distance r from the axis and hence considered as a small differential mass dm. Let the thickness of the segment be dr. The mass per unit area of the quadrant

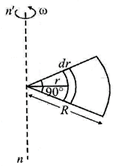\[=\frac{M}{\pi {{R}^{2}}/4}=\frac{4M}{\pi {{R}^{2}}}\]

Area of segment \[=\frac{1}{4}[\pi {{(r+dr)}^{2}}-\pi {{r}^{2}}]=\frac{1}{4}\times 2\pi rdr=\frac{\pi rdr}{2}\]

\[\therefore \]Mass of the segment, \[dm=\frac{\pi rdr}{2}\times \frac{4M}{\pi {{R}^{2}}}=\frac{2M}{{{R}^{2}}}rdr\]

\[\therefore \] M.I. of this segment about \[nn'\]\[=\left( \frac{2M}{{{R}^{2}}}rdr \right)\times {{r}^{2}}=\frac{2M}{{{R}^{2}}}\times {{r}^{3}}dr\]

\[\therefore \] M.I. of the quadrant about \[nn'\]\[=\int_{0}^{R}{\frac{2M}{{{R}^{2}}}\times {{r}^{3}}dr=\frac{2M}{{{R}^{2}}}\times \frac{{{R}^{4}}}{4}=\frac{M{{R}^{2}}}{2}}\]