A) 23.8 cm of mercury flows out
B) 27.8 cm of mercury flows out
C) 32.8 cm of mercury flows out
D) None of these
Correct Answer: A
Solution :
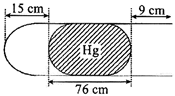
| In horizontal position |
| Length of mercury thread = 76 cm |
| Length of air trapped =15 cm |
| Let area of C.S.\[=1{{\operatorname{cm}}^{2}}\]then \[{{V}_{1}}=15c{{m}^{3}}\] |
 |
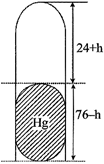 |
| When the tube is held vertically, 15 cm air gets another 9 cm of air and let h cm of mercury flows out to balance the atmospheric pressure. |
| Now height of air column = (24 + h) |
| Height of mercury column = (76-h) |
| Then pressure of air = 76-(76-h) = h cm. of mercury |
| At constant temperature, |
| \[{{\operatorname{P}}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}\] |
| \[76\times 15=h(24+h)\] |
| Or \[{{h}^{2}}+24h-1140=0\] |
| On solvings, h=23.8cm. Or -47.8cm. |
| Neglecting negative, \[h=23.8cm.\] |
| i.e., \[23.8cm.\]Of mercury flows out. |
You need to login to perform this action.
You will be redirected in
3 sec
