question_answer

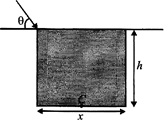
A student sees the top edge and the bottom centre \[C\] of a pool simultaneously from an angle \[\theta \] above the horizontal as shown in the figure.

The refractive index of water which fills up to the top edge of the pool is \[\frac{4}{3}.\operatorname{if}\frac{h}{x}=\frac{7}{4},\] then \[\theta \]is

A) \[\frac{2}{7}\]

B) \[\frac{8}{3\sqrt{45}}\]

C) \[\frac{8}{3\sqrt{53}}\]

D) \[\frac{8}{21}\]

Correct Answer: C

Solution :

Ray diagram for pool is as shown below.
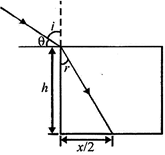Using \[{{n}_{1}}.\sin i={{n}_{2}}.\sin \,r,\]we have
\[1\times \sin (90{}^\circ -\theta )=\frac{4}{3}\sin \,r\]	? (i)
Also,     \[\tan r=\frac{x}{2h}=\frac{4}{7\times 2}=\frac{2}{7}\]\[\Rightarrow \]     \[\sin r=\frac{2}{\sqrt{53}}\]
Substituting sin \[r\]in Eq. (i), we have
\[\cos \,\theta =\frac{4}{3}\times \frac{2}{\sqrt{53}}=\frac{8}{3\sqrt{53}}\]