question_answer

A cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the factional force acting on the cylinder are

A) up the incline while ascending and down the incline descending.

B) Up the incline while ascending as well as descending.

C) Down the incline while ascending and up the incline while descending.

D) Down the incline while ascending as well as descending.

Correct Answer: B

Solution :

Imagine the cylinder to be moving on a frictionless surface. In both the cases the acceleration of the centre of mass of the cylinder is\[g\sin \theta \]. This is also the acceleration of the point of contact of the cylinder with the inclined surface. Also no torque (about the centre of cylinder) is acting on the cylinder since we assumed the surface to be frictionless and the forces acting on the cylinder is mg and N which  pass through the centre of cylinder. Therefore the net movement of the point of contact in both the cases is in the downward direction as shown. Therefore the frictional force will act in the upward direction in both the cases.

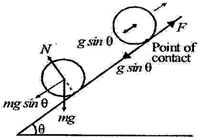Note: In general we find the acceleration of the point of contact due to translational and rotational motion and then find the net acceleration of the point of contact. The frictional force acts in the opposite direction to that of net acceleration of point of contact.