question_answer

An object with uniform density p is attached to a spring that is known to stretch linearly with applied force as shown below.

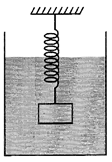When the spring object system is immersed in a liquid of density\[{{\rho }_{1}}\], as shown in the above figure, the spring stretches by an amount\[{{x}_{1}}\]\[\left( \rho >{{\rho }_{1}} \right)\]. When the experiment is repeated in a liquid of density\[\left( {{\rho }_{2}}<{{\rho }_{1}} \right)\], the spring stretches by an amount\[{{x}_{2}}.\]. Neglecting any buoyant force on the spring, the density of the object is

A) \[\rho =\frac{{{\rho }_{1}}{{x}_{1}}-{{\rho }_{2}}{{x}_{2}}}{{{x}_{1}}-{{x}_{2}}}\]

B) \[\rho =\frac{{{\rho }_{1}}{{x}_{2}}-{{\rho }_{2}}{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

C) \[\rho =\frac{{{\rho }_{1}}{{x}_{2}}+{{\rho }_{2}}{{x}_{1}}}{{{x}_{1}}+{{x}_{2}}}\]

D) \[\rho =\frac{{{\rho }_{1}}{{x}_{1}}+{{\rho }_{2}}{{x}_{2}}}{{{x}_{1}}+{{x}_{2}}}\]

Correct Answer: B

Solution :

for equilibrium of block hung from string, spring force+ Buoyant force =weight of block

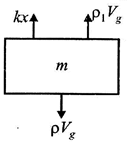So, we have

\[k{{x}_{1}}+{{\rho }_{1}}Vg=\rho Vg...(i)\]

\[\operatorname{and}k{{x}_{2}}+{{\rho }_{2}}Vg=\rho Vg...(ii)\]

Eliminating\[k\], we get

\[\rho =\frac{{{\rho }_{1}}{{x}_{2}}-{{\rho }_{2}}{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]