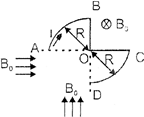
| Wire bent as ABOCD as shown, carries current I entering at A and leaving at D. Three uniform magnetic fields each \[{{B}_{0}}\] exist in the region as shown. The force on the wire is: |
 |
A) \[\sqrt{3}\,I\,R\,{{B}_{0}}\]
B) \[\sqrt{5}\,I\,R\,{{B}_{0}}\]
C) \[\sqrt{8}\,I\,R\,{{B}_{0}}\]
D) \[\sqrt{6}\,I\,R\,{{B}_{0}}\]
Correct Answer: D
Solution :
| \[\vec{F}=\vec{F}=I\vec{\ell }\times \vec{B}\] |
| \[\vec{\ell }=\overrightarrow{AD}=R\,(\hat{i}-\hat{j})\] |
| \[\vec{B}={{B}_{0}}\,(\hat{i}+\hat{j}-\hat{k})\] |
| \[\therefore \] \[\vec{F}=IR{{B}_{0}}\,(\hat{i}-\hat{j})\times (\hat{i}+\hat{j}-\hat{k})=IR{{B}_{0}}\,\,\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ 1 & -1 & 0 \\ 1 & 1 & -1 \\ \end{matrix} \right|\] |
| \[=IR{{B}_{0}}\,(\hat{i}+\hat{j}+2\hat{k})\] |
| \[F=IR{{B}_{0}}\sqrt{6}\] |
| Aliter: |
| \[\vec{B}={{B}_{0}}\,(\hat{i}+\hat{j}-\hat{k})\] |
| \[\vec{\ell }=R\,(\hat{i}-\hat{j})\] |
| \[\vec{B}\,\,\vec{\ell }=0\] \[\Rightarrow \] \[\text{Angle}=90{}^\circ \] \[\Rightarrow \] \[F=BI\ell \] |
| \[=\sqrt{3}{{B}_{0}}I\sqrt{2}\,R=\sqrt{6}{{B}_{0}}IR\] |
You need to login to perform this action.
You will be redirected in
3 sec
