A) \[\frac{a}{3}\]
B) \[\frac{2a}{3}\]
C) \[\frac{a}{6}\]
D) none of these
Correct Answer: A
Solution :
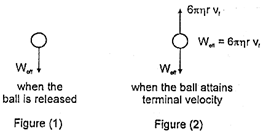  |
| When the ball is just released, the net force on ball is \[{{W}_{eff}}\,(\text{= mg}-\text{buoyant}\,\,\text{force})\] |
| The terminal velocity \['{{v}_{f}}'\] of the ball is attained when net force on the ball is zero. |
| \[\therefore \] Viscous force \[6\,\pi \,\eta \,r\,{{v}_{f}}={{W}_{eff}}\] |
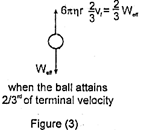
| When the ball acquires \[\frac{2}{3}rd\] of its maximum velocity \[{{v}_{f}}\] |
| the viscous force is \[=\frac{2}{3}{{W}_{eff}}.\] |
| Hence net force is \[{{W}_{eff}}-\frac{2}{3}{{W}_{eff}}=\frac{1}{3}{{W}_{eff}}\] |
| \[\therefore \] required acceleration is \[=\frac{a}{3}\] |
You need to login to perform this action.
You will be redirected in
3 sec
