question_answer

If \[\left| \overrightarrow{a}+\overrightarrow{b} \right|=\left| \overrightarrow{a}-\overrightarrow{b} \right|\] then the vectors \[\vec{a}\]and \[\vec{b}\]are adjacent sides of

A) a rectangle

B) a square

C) a rhombus

D) none of these

Correct Answer: A

Solution :

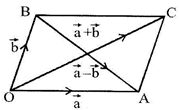Let \[\overrightarrow{OA}=\overrightarrow{a}\] and \[\overrightarrow{OB}=\overrightarrow{b}\]. Complete the parallelogram OACB.

\[\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\] \[\Rightarrow \left| \overrightarrow{a}+\overrightarrow{b} \right|=OC\]

Again \[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}\] \[\Rightarrow \left| \overrightarrow{a}-\overrightarrow{b} \right|=BA\]

Given \[\left| \overrightarrow{a}+\overrightarrow{b} \right|=\left| \overrightarrow{a}-\overrightarrow{b} \right|\Rightarrow \operatorname{OC}=BA\]

\[\therefore \]Diagonals of the parallelogram OACB are equal.

\[\therefore \]\[\overrightarrow{\operatorname{a}}\]and \[\overrightarrow{\operatorname{b}}\]are adjacent sides of a rectangle.