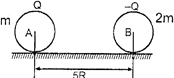
| Two smooth spherical non conducting shells each of radius R having uniformly distributed charge \[Q\And -\,Q\] on their surfaces are released on a smooth non-conducting surface when the distance between their centres is 5 R. The mass of A is m and that of B is 2 m. The speed of A just before A and B collide is: |
| [Neglect gravitational interaction] |
| \[(take\,\,K=\frac{1}{4\pi {{\in }_{0}}})\] |
 |
A) \[\sqrt{\frac{2\,k{{Q}^{2}}}{5\,mR}}\]
B) \[\sqrt{\frac{4\,k{{Q}^{2}}}{5\,mR}}\]
C) \[\sqrt{\frac{8\,k{{Q}^{2}}}{5\,mR}}\]
D) \[\sqrt{\frac{16\,k{{Q}^{2}}}{5\,mR}}\]
Correct Answer: A
Solution :
| From conservation of momentum, if speed of sphere A is v, then speed of sphere B is \[\frac{v}{2}.\] |
| From conservation of energy\[\frac{1}{2}m{{v}^{2}}+\frac{1}{2}(2m)\,\,{{\left( \frac{v}{2} \right)}^{2}}=\frac{-\,k{{Q}^{2}}}{5R}+\frac{k{{Q}^{2}}}{2R}\]or \[\frac{3}{4}m{{v}^{2}}=\frac{3}{10}\frac{k{{Q}^{2}}}{R}\] |
| or \[v=\sqrt{\frac{2}{5}\frac{k{{Q}^{2}}}{mR}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
