A) \[75\times {{10}^{-13}}\]
B) \[75\times {{10}^{-12}}\]
C) \[7.5\times {{10}^{-12}}\]
D) \[7.5\times {{10}^{-13}}\]
Correct Answer: D
Solution :
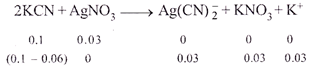 |
| \[\therefore \]\[{{[Ag{{(CN)}_{2}}]}^{-}}=0.03M\] |
 |
| Since,\[{{\operatorname{K}}_{c}}\] is too small and dissociation of |
| \[\operatorname{Ag}\left( CN \right)_{2}^{-}\]is very less and thus, |
| \[\therefore \]\[0.04+2a\approx 0.04\text{ }\operatorname{and}\text{ }0.03-a\approx 0.03\] |
| \[\therefore \]\[{{[Ag{{(CN)}_{2}}]}^{-}}=0.03;[A{{g}^{+}}]=a,;[C{{N}^{-}}]=0.04\] |
| Now \[{{K}_{C}}=\frac{[A{{g}^{+}}]{{[C{{N}^{-}}]}^{2}}}{[Ag(CN)_{2}^{-}]}=\frac{a\times {{(0.04)}^{2}}}{0.03}\] |
| \[\therefore \] \[a=7.5\times {{10}^{-13}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
