question_answer

A plane mirror is placed at x = 0 with its plane parallel to the y-axis. An object starts from x = 3 m and moves with a velocity of \[(2\hat{i}+2\hat{j})m{{s}^{-1}}\] away from the mirror The relative velocity of the image with respect to the object is

A) \[2\sqrt{2}\,m{{s}^{-1}}\] making an angle of \[45{}^\circ \] with the \[+x\] axis

B) \[2\sqrt{2}\,m{{s}^{-1}}\] making an angle of \[135{}^\circ \] with the \[+x\] axis

C) \[4\text{ }m{{s}^{-1}}\] along the \[-x\] axis

D) \[4\text{ }m{{s}^{-1}}\] along the \[+x\] axis

Correct Answer: C

Solution :

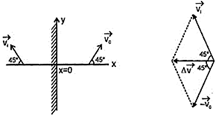Velocity of the object is \[{{\overrightarrow{v}}_{_{0}}}=(2\hat{i}+2\hat{j})m{{s}^{-1}}\]

\[\therefore \]Speed of object is \[{{v}_{i}}=\sqrt{{{2}^{2}}+{{2}^{2}}}=2\sqrt{2}m{{s}^{-1}}\]

=speed of the image\[({{v}_{i}})\]. The velocity \[{{\overrightarrow{v}}_{1}}\]of the image will be as shown in fig. the relative velocity of the image with respect to the object is

\[\Delta \overrightarrow{v}={{\overrightarrow{v  }}_{1}}-{{\overrightarrow{v}}_{0}}={{\overrightarrow{v}}_{1}}+(-{{\overrightarrow{v}}_{0}})\]

\[={{\left[ {{\left( 2\sqrt{2} \right)}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}} \right]}^{1/2}}=4\,m{{s}^{-1}}\,\,along-x\,\,axis.\]