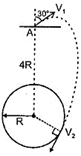
| A particle is projected from point A, that is at a distance 4R from the centre of the earth, with speed \[{{V}_{1}}\] in a direction making \[30{}^\circ \] with the line joining the centre of the earth and point A, as shown. Find the speed \[{{V}_{1}}\] if particle grazes the surface of the earth as shown in figure. Consider gravitational interaction only between these two. \[(use\,\,\frac{GM}{R}=6.4\times {{10}^{7}}{{m}^{2}}/{{s}^{2}})\] |
 |
A) \[4\sqrt{2}\,km/s\]
B) \[3\sqrt{2}\,km/s\]
C) \[6\sqrt{2}\,km/s\]
D) \[5\sqrt{2}\,km/s\]
Correct Answer: A
Solution :
| Conserving angular momentum w.r.t. centre of earth \[m.({{V}_{1}}\cos 60{}^\circ ).4R=m.{{V}_{2}}.R\,\,;\,\,\frac{{{V}_{2}}}{{{V}_{1}}}=2.\] |
| Conserving mechanical energy of the system |
| \[m.({{V}_{1}}\cos 60{}^\circ ).4R=m.{{V}_{2}}.R\]; \[\frac{{{V}_{2}}}{{{V}_{1}}}=2.\] |
| \[-\frac{G\,\,Mm}{4R}+\frac{1}{2}mV_{1}^{2}=-\frac{GMm}{R}+\frac{1}{2}mV_{2}^{2}\] |
| \[\frac{1}{2}{{V}_{2}}^{2}-\frac{1}{2}{{V}_{1}}^{2}=\frac{3}{4}\frac{GM}{R}\]or \[{{V}_{1}}^{2}=\frac{1}{2}\frac{GM}{R}\] |
| \[{{V}_{1}}=\frac{1}{\sqrt{2}}\sqrt{64\times {{10}^{6}}}=\frac{8000}{\sqrt{2}}m/s=4\sqrt{2}km/s\] |
You need to login to perform this action.
You will be redirected in
3 sec
