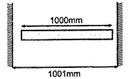
| A rod of length 1000 mm and co-efficient of linear expansion \[a={{10}^{-4}}\] per degree is placed symmetrically between fixed walls separated by 1001 mm. The Young's modulus of the rod is \[{{10}^{11}}\text{ }N/{{m}^{2}}\]. If the temperature is increased by \[20{}^\circ C\,\], then the stress developed in the rod is (in\[N/{{m}^{2}}\]): |
 |
A) 10
B) \[{{10}^{8}}\]
C) \[2\times {{10}^{8}}\]
D) cannot be calculated
Correct Answer: B
Solution :
| The change in length of rod due to increase in temperature in absence of walls is |
| \[\Delta \ell =\ell \alpha \Delta T\]\[=1000\times {{10}^{-4}}\times 20\,mm\]\[=2\,mm\] |
| But the rod can expend upto 1001 mm only. |
| At that temperature its natural length is = 1002 mm. |
| \[\therefore \] compression = 1 mm |
| \[\therefore \] mechanical stress = \[Y\frac{\Delta \ell }{\ell }={{10}^{11}}\times \frac{1}{1000}\] |
| \[={{10}^{8}}N/{{m}^{2}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
