question_answer

Let O be an interior point of \[\Delta ABC\] such that \[OA+2OB+3OC=O.\] Then, the ratio of area of \[\Delta ABC\] to area of\[\Delta AOC\] is

A) 1 : 3                             

B) 3 : 1  

C) 2 : 8                             

D) 3 : 2

Correct Answer: B

Solution :

[b]

\[\frac{\text{Area}\,\text{of}\,\Delta ABC}{\text{Area}\,\text{of}\,\Delta OAC}\]\[=\frac{\frac{1}{2}[|OA\times OB|+|OB\times OC|+|OC\times OA|}{\frac{1}{2}|OA\times OC|}\]\[=\frac{|OA\times OB|+OB\times OC|}{|OA\times OC|}+1\]

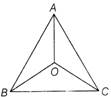Given,  \[OA+2OB+3OC=0\]

\[2OB\times OA+3OC\times OA=0\]

\[\Rightarrow \]\[\frac{|OB\times OA|}{3}=\frac{|OC\times OA|}{2}=\lambda \]

\[OB\times OA+3OB\times OC=0\]

\[\Rightarrow \]\[\frac{|OB\times OA|}{3}=\frac{|OB\times OC|}{1}=\lambda \]

\[\frac{\text{Area}\,\text{of}\,\Delta ABC}{\text{Area}\,\text{of}\,\Delta AOC}=\frac{3\lambda +\lambda }{2\lambda }+1=3:1\]