question_answer

In a \[\Delta ABC\] bisector of \[\angle C\] meets the side AB at D and circumcentre at E. The maximum value of \[CD\cdot DE\] is equal to

A) \[\frac{{{a}^{2}}}{4}\]                                   

B) \[\frac{{{b}^{2}}}{4}\]

C) \[\frac{{{c}^{2}}}{4}\]           

D) \[\frac{{{(a+b)}^{2}}}{4}\]

Correct Answer: C

Solution :

[c]

\[AB=c\]

\[BC=a\]

\[AC=b\]

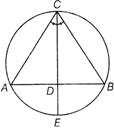\[AD+DB=AB=c\]

\[CD\times DE=AD\times BD\]

\[\frac{AD+DB}{2}\ge \sqrt{AD\times BD}\]                     \[[\because \,\,\,\,\,AB\ge 4M]\]

\[\frac{c}{2}\ge \sqrt{CD\times DE}\]                   \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,CD\times DE\le \frac{{{c}^{2}}}{4}\]