question_answer

Two infinitely long charge wires with linear densities \[\lambda \] & \[3\lambda \] are placed along x & y axis respectively determined the \[\tan \theta \] where \[\theta \] is the angle that electric field at any point on the line \[y=\sqrt{3}\,\,x\] make with positive x-axis.

A) \[3\sqrt{3}\]                  

B) \[\frac{\sqrt{3}}{3\sqrt{2}}\]

C) \[\frac{1}{3\sqrt{3}}\]

D) \[\sqrt{3}\]

Correct Answer: C

Solution :

[C]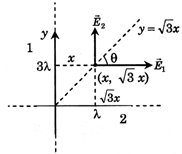

Electric field due to long wire is \[\frac{\lambda }{2\pi {{\in }_{0}}r'}\]

There are two wire one along x and one along y axis

So net \[E={{\vec{E}}_{1}}+{{\vec{E}}_{2}}\] where \[{{E}_{1}}\] and \[{{E}_{2}}\] is electric field due to each wire

Where \[{{\vec{E}}_{2}}=\frac{\lambda }{2\pi {{\in }_{0}}\sqrt{3}x}\hat{j},\] \[{{\vec{E}}_{1}}=\frac{3\lambda }{2\pi {{\in }_{0}}x}\hat{i}\]\[\vec{E}=\frac{3\lambda }{2\pi {{\in }_{0}}x}\hat{i}+\frac{\lambda }{2\pi {{\in }_{0}}x\sqrt{3}}\hat{j}\]

\[\theta \] is the angle that \[{{E}_{net}}\]made by positive x- axis

\[\tan \theta =\frac{{{E}_{y}}}{{{E}_{x}}}=\frac{1}{\sqrt{3}}\div 3=\frac{1}{3\sqrt{3}}\]