
A) \[\frac{\lambda R}{{{\in }_{0}}}\]
B) \[\frac{\lambda R}{2{{\in }_{0}}}\]
C) \[\frac{\lambda \pi R}{4{{\in }_{0}}}\]
D) \[\frac{\lambda \pi R}{3{{\in }_{0}}}\]
Correct Answer: D
Solution :
[D] Flux will be maximum when maximum length of ring is inside the sphere. This will occur when the chord AB is maximum Now maximum length of chord AB = diameter of sphere. In this case one arc of ring inside the sphere subtends an angle of\[\pi /3\] at the center of ring.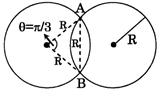 \[\therefore \] Charge on this are arc\[=\lambda \times \] length of arc \[\therefore \] Charge on this arc =\[\frac{R\pi }{3}\lambda \] \[\therefore \,\,\,\phi =\frac{\frac{R\pi \lambda }{3}}{{{\in }_{0}}}=\frac{R\pi \lambda }{3{{\in }_{0}}}\]
\[\therefore \] Charge on this are arc\[=\lambda \times \] length of arc \[\therefore \] Charge on this arc =\[\frac{R\pi }{3}\lambda \] \[\therefore \,\,\,\phi =\frac{\frac{R\pi \lambda }{3}}{{{\in }_{0}}}=\frac{R\pi \lambda }{3{{\in }_{0}}}\]
You need to login to perform this action.
You will be redirected in
3 sec
