A) \[\frac{\lambda }{2\pi {{\in }_{0}}}\,\,\ell n\,\,\frac{13}{5}\]
B) \[\frac{2\lambda }{\pi {{\in }_{0}}}\,\,\ell n\,\,\frac{13}{3}\]
C) \[\frac{\lambda }{4\pi {{\in }_{0}}}\,\,\ell n\,\,\frac{13}{5}\]
D) \[-\,\frac{\lambda }{2\pi {{\in }_{0}}}\,\,\ell n\,\,\frac{13}{5}\]
Correct Answer: A
Solution :
[A] 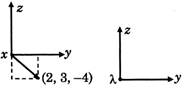 |
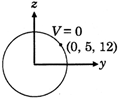
| Perpendicular distance of A (0, 5, 12) from x axis\[={{r}_{1}}=13\] & \[B=(2,3,-\,4)\] from x axis \[{{r}_{2}}=5\] and potential difference between these two point is \[=\frac{\lambda }{2\pi {{\in }_{0}}}\] In \[\frac{13}{5}\] |
| \[{{V}_{B}}-{{V}_{A}}=\frac{\lambda }{2\pi {{\in }_{0}}}\,\,In\,\,\frac{13}{5}\] |
| \[{{V}_{A}}=0\] |
| \[\therefore \,\,\,{{V}_{B}}=\frac{\lambda }{2\pi {{\in }_{0}}}\,\,In\,\,\frac{13}{5}\] |
| Potential at \[(2,3,-\,4)=\frac{\lambda }{2\pi {{\in }_{0}}}\,\,In\,\,\frac{13}{5}\] |
You need to login to perform this action.
You will be redirected in
3 sec
