A) 124 V
B) 133 V
C) 100 V
D) 200 V
Correct Answer: B
Solution :
[B] 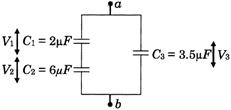 | |
| Let potential applied between a and b = V using the formula | |
| \[{{V}_{1}}=\,\,\,\frac{\frac{1}{2}}{\frac{1}{2}+\frac{1}{6}}\,\,\times \,\,V\] | \[{{V}_{2}}=\,\,\frac{\frac{1}{6}}{\frac{1}{2}+\frac{1}{6}}\,\,\times \,\,V\] |
| \[{{V}_{1}}=\frac{6}{8}\,\,\times \,\,V=\frac{3}{4}V\] | \[{{V}_{2}}=\frac{1}{4}V,\] \[{{V}_{3}}=V\] |
| These voltage should be less than corresponding break down voltage | |
| \[\left. \begin{matrix} Now\,\,\,\frac{3}{4}V<100 & \Rightarrow V<\frac{400}{3} \\ \frac{V}{5}<50 & \Rightarrow V<200V \\ V<400 & \Rightarrow V<400 \\ \end{matrix} \right\}\begin{matrix} common\,\,solution \\ V<\frac{400}{3} \\ V<133\,\,V \\ \end{matrix}\] | |
You need to login to perform this action.
You will be redirected in
3 sec
