question_answer

Two blocks of equal mass are tied with a light string, which passes over a massless pulley as shown in figure. The magnitude of acceleration of centre of mass of both the blocks is (neglect friction everywhere, inclined wedge is fixed at floor) -

A) \[\left( \frac{\sqrt{3}-1}{4\sqrt{2}} \right)g\]         

B) \[(\sqrt{3}-1)g\]

C) \[\frac{g}{2}\]                           

D) \[\left( \frac{\sqrt{3}-1}{\sqrt{2}} \right)g\]

Correct Answer: A

Solution :

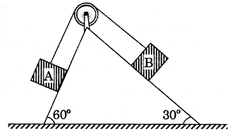
[A]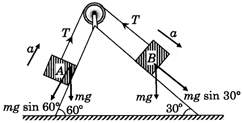

NLM on B         \[mg\sin 30{}^\circ -T=m\times a\]                      ?(1)

\[T-mg\,\,\sin 60{}^\circ =ma\]                                                   ?(2)

\[a=\frac{mg\,\,\sin 60{}^\circ -mg\,\,\sin 30{}^\circ }{2m}\]

Where a is Acceleration of system Here, m=mass of each block  or \[a=\left( \frac{\sqrt{3}-1}{4} \right)g\]

Acceleration of center of mass \[\to {{a}_{com}}\]

Now \[\to {{\overrightarrow{a}}_{\,com}}=\frac{m{{\overrightarrow{\,a}}_{1}}+m\,{{\overrightarrow{a}}_{2}}}{2m}\]

Here, \[{{\overrightarrow{a}}_{1}}\] and \[{{\overrightarrow{a}}_{2}}\]are at \[\left( \frac{\sqrt{3}-1}{4} \right)g\]right angles.

Hence, \[\left| \to {{\overrightarrow{a}}_{com}} \right|=\frac{\sqrt{2}}{2}a=\left( \frac{\sqrt{3}-1}{4\sqrt{2}} \right)g\]