A) \[\left( \frac{{{v}_{0}}}{2{{B}_{0}}\alpha },\frac{\sqrt{2}{{v}_{0}}}{\alpha {{B}_{0}}},\frac{-{{v}_{0}}}{{{B}_{0}}\alpha } \right)\]
B) \[\left( -\frac{{{v}_{0}}}{2{{B}_{0}}\alpha },0,0 \right)\]
C) \[\left( 0,\frac{2{{v}_{0}}}{{{B}_{0}}\alpha },\frac{{{v}_{0}}\pi }{2{{B}_{0}}\alpha } \right)\]
D) \[\left( \frac{{{v}_{0}}\pi }{{{B}_{0}}\alpha },0,\frac{-2{{v}_{0}}}{{{B}_{0}}\alpha } \right)\]
Correct Answer: B
Solution :
[D] Radio of projection of helix will be \[r=\frac{{{v}_{0}}}{\alpha {{B}_{0}}}\] and time period of projection will be \[T=\frac{2\pi }{\alpha {{B}_{0}}},\] projected circle will be formed on \[y-z\] plane. It will make half circle in time \[t=\frac{\pi }{{{B}_{0}}\alpha }.\]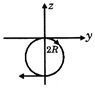 x-coordinate = \[{{v}_{0}}t={{v}_{0}}.\frac{\pi }{{{B}_{0}}\alpha }.\]
x-coordinate = \[{{v}_{0}}t={{v}_{0}}.\frac{\pi }{{{B}_{0}}\alpha }.\]
You need to login to perform this action.
You will be redirected in
3 sec
