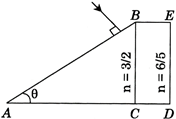
A) \[\theta \le 37{}^\circ \]
B) \[\theta <37{}^\circ \]
C) \[\theta \le 53{}^\circ \]
D) \[\theta <53{}^\circ \]
Correct Answer: C
Solution :
[B] \[A=90-\theta \] \[{{r}_{2}}=A=90-\theta >{{\theta }_{C}}\] \[\cos \theta >\sin {{\theta }_{C}}=\frac{6/5}{3/2}=\frac{4}{5}\] \[\Rightarrow \theta <{{\cos }^{-1}}\frac{4}{5}=37{}^\circ .\]You need to login to perform this action.
You will be redirected in
3 sec
