question_answer

A metal bar (length L, mass m) can slides over two connected rails fitted over an inclined plane without friction. Rails are of very less resistance and metal bar is of resistance R. When a magnetic field B is switch ON perpendicular to ground, then terminal speed of the metal bar obtained is

A) \[\frac{Rmg}{{{B}^{2}}{{L}^{2}}}\]            

B)  \[\frac{Rmg}{{{B}^{2}}{{L}^{2}}}.\sec \theta .\tan \theta \]

C) \[\frac{Rmg}{{{B}^{2}}{{L}^{2}}}.\tan \theta \]                    

D) \[\frac{Rmg}{{{B}^{2}}{{L}^{2}}}.cot\theta \]

Correct Answer: B

Solution :

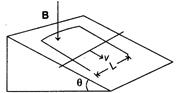
Due to motion of bar in magnetic field, emf induced, \[E=Bl\upsilon =BL\upsilon \cos \theta \]

Current in metal bar,  \[I=\frac{E}{R}=\frac{BL\upsilon }{R}\cos \theta \]

Force on bar up the inclined plane is \[F=BIL\cos \theta =\frac{{{B}^{2}}{{L}^{2}}\upsilon }{R}{{\cos }^{2}}\theta \]

When this force is equal to downwards gravitational pull, bar reaches terminal speed.

\[\frac{{{B}^{2}}{{L}^{2}}\upsilon {{\cos }^{2}}\theta }{R}=mg\sin \theta \]

\[\upsilon =\frac{Rmg}{{{B}^{2}}{{L}^{2}}}=\sec \theta .\tan \theta \]