question_answer

From a fixed point \[A\] on the circumference of a circle of radius \[r,\] the perpendicular \[AY\] is let fall on the tangent at \[P.\] the maximum area of the triangle \[APY\]is

A) \[{{r}^{2}}\]

B) \[\frac{3\sqrt{3}}{4}{{r}^{2}}\]

C) \[\frac{3\sqrt{3}}{8}{{r}^{2}}\]

D) \[\sqrt{3{{r}^{2}}}\]

Correct Answer: C

Solution :

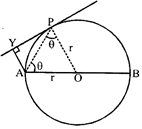
See that figure since,\[OP\bot PY\]

\[\therefore \angle APY=90{}^\circ -\theta \]

Where \[OPA=\theta \]

\[\therefore \angle PAY=\theta \]

Now in \[\Delta OPA,\]

\[A{{P}^{2}}={{r}^{2}}+{{r}^{2}}-2r.r\cos (\pi -2\theta )=4{{r}^{2}}{{\cos }^{2}}\theta \]

\[\therefore AP=2r\cos \theta \]

\[\Rightarrow PY=AP\sin \theta =r\sin 2\theta \]

\[and\,AY=AP\cos \theta =2r\,{{\cos }^{2}}\theta \]

\[\therefore \]Area of \[\Delta APY,\]

\[\Delta =\frac{1}{2}PY.AY={{r}^{2}}\sin 2\theta {{\cos }^{2}}\theta \]

\[\frac{d\Delta }{d\theta }={{r}^{2}}\left[ 2\cos 2\theta {{\cos }^{2}}\theta -{{\sin }^{2}}2\theta  \right]=0\]

\[\Rightarrow \theta =\frac{\pi }{2},\frac{\pi }{6}\]

\[\because 0\ne \frac{\pi }{2}.\]

Also \[\Delta \] is maximum at \[\theta =\frac{\pi }{6}\](check)

\[\therefore {{\Delta }_{\max }}={{r}^{2}}.\frac{\sqrt{3}}{2}{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}=\frac{3\sqrt{3{{r}^{2}}}}{8}\]