question_answer

Find the equation of plane determined

by points \[A(3,\,\,-\,1,\,\,2),\] B(5, 2, 4), \[C(-\,1,\,\,-\,1,\,\,6)\] and hence find the distance between plane and point P(6, 5, 9).

OR

Show that the lines

\[\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+\lambda (\hat{i}+2\hat{j}+2\hat{k})\] and

\[\vec{r}=5\hat{i}-2\hat{j}+\mu (3\hat{i}+2\hat{j}+6\hat{k})\] are intersecting.

Hence, find their point of intersection.

Answer:

Given points are \[A\,(3,\,\,-1,\,\,2),\]\[B\,(5,\,\,2,\,\,4)\]and\[C\,(-\,1,\,\,-\,1,\,\,6)\].

Now, equation of plane passing through A, B and C is

given by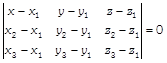

\[\Rightarrow \]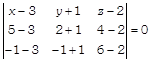

\[\Rightarrow \]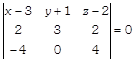

Expanding along \[{{R}_{1}}\]we get

\[(x-3)\,\,(12-0)-(y+1)\,\,(8+8)+(z-2)\,\,(0+12)=0\]\[\Rightarrow \]    \[12x-36-16y-16+12z-24=0\]

\[\Rightarrow \]   \[12x-16y+12z=76\]

\[\Rightarrow \]   \[3x-4y+3z=19\]

Now, distance of the point (6, 5, 9) from the plane (i) is

\[d=\left| \frac{3\,(6)-4\,(5)+3\,(9)-19}{\sqrt{{{3}^{2}}+{{4}^{2}}+{{3}^{2}}}} \right|\]

\[=\left| \frac{18-20+27-19}{\sqrt{9+16+9}} \right|\]

\[=\left| \frac{6}{\sqrt{34}} \right|\]

\[=\frac{6}{\sqrt{34}}units\]

Or

Consider the lines

\[\overrightarrow{r}=3\,\hat{i}+2\,\hat{i}-4\hat{k}+\lambda \,(\hat{i}+2\hat{j}+2\hat{k})\]               ?(i)

and       \[\overrightarrow{r}=5\,\hat{i}-2\hat{j}+\mu \,(3\,\hat{i}+2\hat{j}+6\hat{k})\]        ?(ii)

Here,     \[{{\overrightarrow{a}}_{1}}=3\,\hat{i}-2\hat{j}-4k,\,\,{{\overrightarrow{b}}_{1}}=\hat{i}+2\hat{j}+2\hat{k}\]

and       \[{{\overrightarrow{a}}_{2}}=5\,\hat{i}-2\hat{j},\,\,{{\overrightarrow{b}}_{2}}=3\,\hat{i}+2\hat{j}+6\hat{k}\]

\[\therefore \]      \[{{\overrightarrow{a}}_{2}}-{{\overrightarrow{a}}_{1}}=5\,\hat{i}-2\hat{j}-3\,\hat{i}-2\hat{j}+4\hat{k}\]

\[=2\hat{i}-4\hat{j}+4\hat{k}\]

and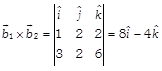

Consider\[({{\overrightarrow{a}}_{2}}-{{\overrightarrow{a}}_{1}})\cdot ({{\overrightarrow{b}}_{1}}\times {{\overrightarrow{b}}_{2}})=16-16=0\]

As \[({{\overrightarrow{a}}_{2}}-{{\overrightarrow{a}}_{1}})\cdot ({{\overrightarrow{b}}_{1}}\times {{\overrightarrow{b}}_{2}})=0\]

\[\Rightarrow \]Lines are intersecting (coplanar and \[{{\overrightarrow{b}}_{1}}\ne {{\overrightarrow{b}}_{2}}\])

General point on line (i) is

\[\overrightarrow{r}=(3+\lambda )\,\hat{i}+(2+2\lambda )\hat{j}+(-\,4+2\lambda )\hat{k}\]           ?(iii)

General point on line (ii) is

\[\overrightarrow{r}=(5+3\mu )\,\hat{i}+(-\,2+2\mu )\hat{j}+6\mu \hat{k}\]          ?(iv)

If Eqs. (iii) and (iv) represent same point

\[3+\lambda =5+3\mu \Rightarrow \lambda -3\mu =2\]       ?(v)

\[2+2\lambda =-\,2+2\mu \]

\[\Rightarrow \]               \[2\lambda -2\mu =-\,4\]

and                   \[-\,4+2\lambda =6\mu \]

\[\Rightarrow \]               \[2\lambda -6\mu =4\]                ?(vi)

On solving Eqs. (vi) and (vii), we get

\[\lambda =-\,4,\]\[\mu =-\,2\]

On putting the values of \[\lambda \] and \[\mu \] in Eq. (v), we get

\[-\,4+6=2\]                  [true]

Hence, for \[\lambda =-\,4,\]\[\mu =-\,2,\]Eqs. (iii) and (iv) represent the same point.

Position vector of point of intersection is\[\overrightarrow{r}=-\,\hat{i}-6\hat{j}-12\hat{k}\]

\[\therefore \]Point of intersection is \[(-\,1,\,\,-\,6,\,\,-\,12)\]