question_answer

Find the image of point (1, 0, 0) on the line \[\frac{x}{1}=\frac{y}{2}=\frac{z}{3}.\]

OR

Find the equation of the plane that contains the point \[(1,\,\,-\,1,\,\,2)\] and is perpendicular to both the planes \[2x+3y-2z=5\]and \[x+2y-3z=8.\]

Hence, find the distance of point \[P(-\,2,\,\,5,\,\,5)\] from the plane obtained above.

Answer:

Let P' (x, y, z) be the image of point P(1, 0, 0) and M be the foot of perpendicular PM on the line AB.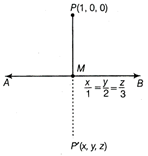

Given equation of line AB is

\[\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\lambda \,(say)\]

\[x=\lambda ,\] \[y=2\lambda \] and \[z=3\lambda \]

\[\therefore \] Coordinates of M are \[(\lambda ,\,\,2\lambda ,\,\,3\lambda )\] for some

\[\lambda \in R.\]                                    ?(i)

Now, DR's of PM are \[\lambda -1,\] \[2\lambda \] and \[3\lambda \] and DR's of AB are 1, 2 and 3

\[\because \]       \[PM\bot AB\]

\[\therefore \]      \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\]

\[\Rightarrow \]   \[1(\lambda -1)+2(2\lambda )+3(3\lambda )=0\]

\[[\because \,\,\,{{a}_{1}}=1,\,\,{{b}_{1}}=2,\,\,{{c}_{1}}=3,\,\,{{a}_{2}}=(\lambda -1),\]

\[{{b}_{2}}=2\lambda ,\,\,{{c}_{2}}=3\lambda ]\]

\[\Rightarrow \]   \[\lambda -1+4\lambda +9\lambda =0\] \[\Rightarrow \] \[14\lambda -1=0\]

\[\Rightarrow \]   \[\lambda =\frac{1}{14}\]

Thus, the coordinates of point M are \[\left( \frac{1}{14},\,\,\frac{1}{7},\,\,\frac{3}{14} \right).\]

Now, as M is the mid-point of line PP'.

\[\therefore \] Coordinates of M = Mid-point of P (1, 0, 0)

and \[P'(x,\,\,y,\,\,z)=\left( \frac{1+x}{2},\,\,\frac{0+y}{2},\,\,\frac{0+z}{2} \right)=\left( \frac{1+x}{2},\,\,\frac{y}{2},\,\,\frac{z}{2} \right)\]But coordinates of M are \[\left( \frac{1}{14},\,\,\frac{1}{7},\,\,\frac{3}{14} \right)\]

\[\therefore \]      \[\left( \frac{x+1}{2},\,\,\frac{y}{2},\,\,\frac{z}{2} \right)=\left( \frac{1}{14},\,\,\frac{1}{7},\,\,\frac{3}{14} \right)\]

\[\Rightarrow \]   \[\frac{x+1}{2}=\frac{1}{14}\]

\[\Rightarrow \]   \[14x+14=2\]

\[\Rightarrow \]   \[14x=-12\]

\[\Rightarrow \]   \[x=-\,6/7,\]

\[\frac{y}{2}=\frac{1}{7}\] \[\Rightarrow \] \[y=\frac{2}{7}\]

and       \[\frac{z}{2}=\frac{3}{14}\] \[\Rightarrow \] \[z=\frac{3}{7}\]

Hence, the image of point P(1, 0, 0) is \[P'\left( -\frac{6}{7},\,\,\frac{2}{7},\,\,\frac{3}{7} \right).\]

OR

Equation of plane containing the point \[(1,\,\,-\,1,\,\,2)\] is

\[a(x-1)+b(y+1)+c(z-2)=0\]                       ?(i)

\[\because \] Plane (i) is perpendicular to plane

\[2x+3y-2z=5\]

\[\therefore \]      \[2a+3b-2c=0\]                         ..           .(ii)

Also, plane (i) is perpendicular to plane

\[x+2y-3z=8\]

\[\therefore \]      \[a+2b-3c=0\]                           ?(iii)

From Eqs. (ii) and (iii), we get

\[\frac{a}{-\,9+4}=\frac{b}{-\,2+6}=\frac{c}{4-3}\]

\[\Rightarrow \]   \[\frac{a}{-\,5}=\frac{b}{4}=\frac{c}{1}=\lambda \,\,(say)\]

\[\Rightarrow \]   \[a=-\,5\lambda ,\] \[b=4\lambda \] and \[c=\lambda \]

On putting these values in Eq. (i), we get

\[-\,5\lambda (x-1)+4\lambda (y+1)+\lambda (z-2)=0\]

\[\Rightarrow \]   \[-\,5(x-1)+4(y+1)+(z-2)=0\]

\[\Rightarrow \]   \[-\,5x+5+4y+4+z-2=0\]

\[\Rightarrow \]   \[-\,5x+4y+z+7=0\]

\[\Rightarrow \]   \[5x-4y-z-7=0\]               ?(iv)

It is the required equation of plane

Now, ifd is the distance of point \[(-\,2,\,\,5,\,\,5)\] from plane (iv).

Then, \[d=\left| \frac{5\times (-\,2)+(-\,4)\times 5+(-1)\times 5-7}{\sqrt{{{5}^{2}}+{{(-\,4)}^{2}}+(-\,{{1}^{2}})}} \right|\]

\[=\left| \frac{-10-20-5-7}{\sqrt{25+16+1}} \right|\]\[=\frac{42}{\sqrt{42}}=\sqrt{42}\] units.