| Show that \[\Delta ABC\] is an isosceles triangle, if the determinant |
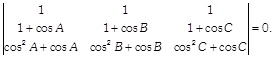 |
| OR |
| If \[A+B+C=\pi ,\] show that |
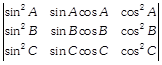 \[=-\sin (A-B)\sin (B-C)\sin (C-A)\] \[=-\sin (A-B)\sin (B-C)\sin (C-A)\] |
Answer:
We have, 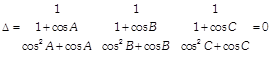
Applying \[{{C}_{1}}\to {{C}_{1}}-{{C}_{3}}\] and \[{{C}_{2}}\to {{C}_{2}}-{{C}_{3}},\] we get 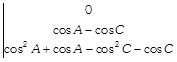
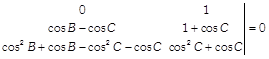
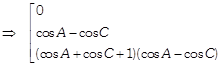
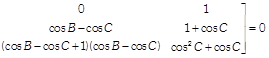
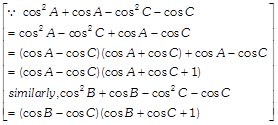
Taking \[(\cos A-\cos C)\]common from \[{{C}_{1}}\] and \[(\cos B-\cos C)\] common from \[{{C}_{2}},\] we get \[(\cos A-\cos C)\cdot (\cos B-\cos C)\] 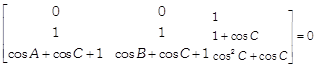
\[\left. \begin{align} & 1 \\ & 1+\cos C \\ & {{\cos }^{2}}C+\cos C \\ \end{align} \right]=0\] \[\Rightarrow \,\,\,\,(\cos A-\cos C)\cdot (\cos B-\cos C)\] \[[(\cos B+\cos C+1)-(\cos A+\cos C+1)]=0\] [Expanding along \[{{R}_{1}}\]] \[\Rightarrow \,\,\,\,\,(\cos A-\cos C)\cdot (\cos B-\cos C)\] \[(\cos B+\cos C+1-\cos A-\cos C-1)=0\] \[\Rightarrow \,\,(\cos A-\cos C)\cdot (\cos B-\cos C)(\cos B-\cos A)=0\]\[\Rightarrow \] \[\cos A=\cos C\,\,\text{or}\,\,\cos B=\cos C\,\,\text{or}\,\,\cos B\] \[=\cos A\] \[\Rightarrow \,\,\,\,A=C\text{ or }B=C\text{ or }B=A\] Hence, ABC is an isosceles triangle. Hence proved. OR The given determinant 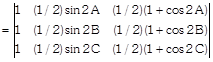 \[[{{C}_{1}}\to {{C}_{1}}+{{C}_{3}}]\]
\[[{{C}_{1}}\to {{C}_{1}}+{{C}_{3}}]\] 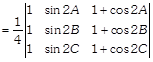
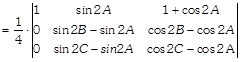
![]()
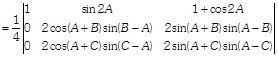
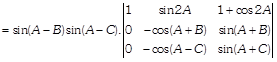
[taking \[2sin(A-B)\] and \[2sin(A\,-C)\] common from \[{{R}_{2}}\] and \[{{R}_{3}}\]respectively] 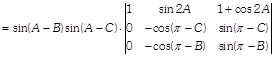 \[[\because \,\,\,A+B+C=\pi ]\]
\[[\because \,\,\,A+B+C=\pi ]\] 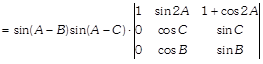
\[=\sin (A-B)\sin (A-C)[\sin B\cos C-\cos B\sin C]\] \[=\sin (A-B)\sin (A-C)\sin (B-C)\] \[=-\sin (A-B)\sin (B-C)\sin (C-A)\]
You need to login to perform this action.
You will be redirected in
3 sec
