A) 5 cm
B) \[\frac{15}{4}\,cm\]
C) \[\frac{10}{3}\,cm\]
D) \[2\,cm\]
Correct Answer: D
Solution :
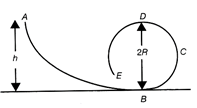
For successful completion of the loop the speed of the body at the lowest point must be at least\[\sqrt{5gR}.\]Conserving Mechanical energy between the position A and B, we get \[mgh=\frac{1}{2}m{{(\sqrt{5gR})}^{2}}\] \[\therefore \] \[h=\frac{5}{2}R\] So, for successful completion of the loop, the value of h must be atleast equal to \[\frac{5}{2}\]R. Or, \[h\ge \frac{5}{2}R\Rightarrow \frac{5R}{2}\le h\] \[\therefore \]\[R\le \frac{2h}{5}=\frac{2\times 5}{5}=2\,cm\] So, the maximum value of R must be equal to 2 cm Hence, the correction option is [d].You need to login to perform this action.
You will be redirected in
3 sec
