question_answer

State Gauss's law in electrostatics. Using this law, derive an expression for the electric field due to a uniformly charged infinite plane sheet.

Answer:

Gauss's law states that the total electric flux linked with a closed surface is equal to \[1/{{\varepsilon }_{0}}\] times total charge, enclosed by that closed (Gaussian) surface, i.e. \[{{\phi }_{E}}=\oint{E\cdot dS=\frac{{{q}_{in}}}{{{\varepsilon }_{0}}}}\] where, \[{{q}_{in}}\]= total charge inside the closed (Gaussian) surface Let us consider, a large plane sheet of charge having surface charge density \[\sigma .\] 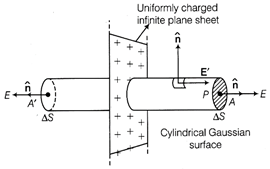Let electric field is to be obtained at a point P at a distance r from it. It is obvious that Gaussian surface will be a cylinder of cross-sectional area A and length 2r with its axis perpendicular to plane sheet of charge. Now, applying Gauss's law over the closed Gaussian surface,             \[\oint_{S}{E\cdot dS}=\frac{q}{{{\varepsilon }_{0}}}\Rightarrow \int_{caps}{E.dS}+\int_{CSA}{E\cdot dS}=\frac{q}{{{\varepsilon }_{0}}}\] Note Closed cylinder comprises of two caps and Curved Surface Area (CSA). \[\int_{caps}{E\,dS\cos 0{}^\circ +\int_{CSA}{E\,dS}\cos 90{}^\circ =\frac{q}{{{\varepsilon }_{0}}}}\] (At caps E and dS are along the same direction whereas \[CSA\,E\bot dS\]) \[\therefore \]      \[E\int_{caps}{dS=\frac{q}{{{\varepsilon }_{0}}}\Rightarrow E\times 2A=\frac{q}{{{\varepsilon }_{0}}}}\] \[\Rightarrow \]   \[E=\frac{q}{2A{{\varepsilon }_{0}}}=\frac{\sigma }{2{{\varepsilon }_{0}}}\]     \[\left[ \because \sigma =\frac{q}{A} \right]\] The direction of E is normal to plane sheet and directed away from sheet (when charge on plate is positive and vice-versa).