| An electron and a positron are released from (0,0,0) and (0,0,1.51R) respectively, in a uniform magnetic field \[B={{B}_{0}}\hat{i},\] each with an equal momentum of magnitude p = eBR. Under what conditions on the direction of momentum will the orbits be non-intersecting circles? |
| Or |
| (i) Explain the elements of Earth's magnetic field and their meaning. Show these elements in a labelled diagram and deduce various relations between them, |
| (ii) Horizontal and vertical components of Earth's magnetic field at a place are 0.15 G and 0.30 G, respectively Calculate the angle of dip and resultant intensity of Earth's magnetic field. |
Answer:
Since, B is along the x-axis, for a circular orbit the momenta of the two particles will be in the y-z plane. Let \[{{p}_{1}}\] and \[{{p}_{2}}\] be the momentum of the electron and positron respectively Both traverse a circle of radius R of opposite sense. Let \[{{p}_{1}}\] make an angle \[\theta \] with the y-axis \[{{P}_{2}}\] must make the same angle. The centres of the respective circles must be perpendicular to the momenta and at a distance R. Let the centre of the electron be at \[{{C}_{e}}\] and of the positron at \[{{C}_{p}}.\] The coordinates of \[{{C}_{e}}\] is 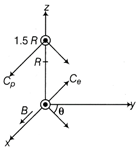 \[{{C}_{e}}\equiv (0,-R\sin \theta ,R\cos \theta )\] The coordinates of \[{{C}_{p}}\] is, \[{{C}_{p}}\equiv (0,-R\,sin\,\theta ,\frac{3}{2}R-R\,cos\,\theta )\] The circles of the two shall not overlap if the distance between the two centres are greater than 2R. Let d be the distance between \[{{C}_{p}}\]and \[{{C}_{e}}.\] Then, \[{{d}^{2}}={{(2R\sin \theta )}^{2}}+{{\left( \frac{3}{2}R-2R\cos \theta \right)}^{2}}\] \[=4{{R}^{2}}{{\sin }^{2}}\theta +\frac{{{9}^{2}}}{4}R-6{{R}^{2}}\cos \theta +4{{R}^{2}}{{\cos }^{2}}\theta \] \[=4{{R}^{2}}+\frac{9}{4}{{R}^{2}}-6{{R}^{2}}\cos \theta \] Since, d has to be greater than 2R, \[{{d}^{2}}>4{{R}^{2}}\] \[\Rightarrow \] \[4{{R}^{2}}+\frac{9}{4}{{R}^{2}}-6{{R}^{2}}\cos \theta >4{{R}^{2}}\Rightarrow \frac{9}{4}>6\,\cos \theta \] or \[\cos \theta <\frac{3}{8}\] Or (i) Elements of Earth's magnetic field The Earth's magnetic field at a place can be described by three parameters known as elements of Earth's magnetic field. They are declination, dip and horizontal component of Earth's magnetic field. (a) Magnetic declination The angle between the geographical meridian and the magnetic meridian at a given place is called the magnetic declination \[(\alpha ).\]
\[{{C}_{e}}\equiv (0,-R\sin \theta ,R\cos \theta )\] The coordinates of \[{{C}_{p}}\] is, \[{{C}_{p}}\equiv (0,-R\,sin\,\theta ,\frac{3}{2}R-R\,cos\,\theta )\] The circles of the two shall not overlap if the distance between the two centres are greater than 2R. Let d be the distance between \[{{C}_{p}}\]and \[{{C}_{e}}.\] Then, \[{{d}^{2}}={{(2R\sin \theta )}^{2}}+{{\left( \frac{3}{2}R-2R\cos \theta \right)}^{2}}\] \[=4{{R}^{2}}{{\sin }^{2}}\theta +\frac{{{9}^{2}}}{4}R-6{{R}^{2}}\cos \theta +4{{R}^{2}}{{\cos }^{2}}\theta \] \[=4{{R}^{2}}+\frac{9}{4}{{R}^{2}}-6{{R}^{2}}\cos \theta \] Since, d has to be greater than 2R, \[{{d}^{2}}>4{{R}^{2}}\] \[\Rightarrow \] \[4{{R}^{2}}+\frac{9}{4}{{R}^{2}}-6{{R}^{2}}\cos \theta >4{{R}^{2}}\Rightarrow \frac{9}{4}>6\,\cos \theta \] or \[\cos \theta <\frac{3}{8}\] Or (i) Elements of Earth's magnetic field The Earth's magnetic field at a place can be described by three parameters known as elements of Earth's magnetic field. They are declination, dip and horizontal component of Earth's magnetic field. (a) Magnetic declination The angle between the geographical meridian and the magnetic meridian at a given place is called the magnetic declination \[(\alpha ).\] 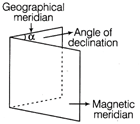 Angle of declination at a place (b) Angle of dip or magnetic inclination The angle made by the Earth's total magnetic field B with the horizontal direction in the magnetic meridian is called angle of dip \[(\delta )\] at that place.
Angle of declination at a place (b) Angle of dip or magnetic inclination The angle made by the Earth's total magnetic field B with the horizontal direction in the magnetic meridian is called angle of dip \[(\delta )\] at that place. 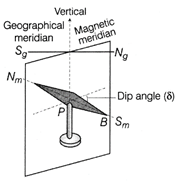 Angle of dip at a place For different places on Earth there is different angle of dip. (c) Horizontal component of Earth's magnetic It is the component of the Earth's total magnetic field (B) in the horizontal direction in the magnetic meridian. If \[\delta \] is the angle of dip at any place, then the horizontal component of Earth's field B at that place is given by \[{{B}_{H}}=B\cos \delta \] At the magnetic equator, \[\delta =0{}^\circ ,\] \[{{B}_{H}}=B\cos 0{}^\circ =B\] At the magnetic poles, \[\delta =90{}^\circ ,\] \[{{B}_{H}}=B\cos 90{}^\circ =0\] Thus, the value of \[{{B}_{H}}\] is different at different places on the surface of the Earth.
Angle of dip at a place For different places on Earth there is different angle of dip. (c) Horizontal component of Earth's magnetic It is the component of the Earth's total magnetic field (B) in the horizontal direction in the magnetic meridian. If \[\delta \] is the angle of dip at any place, then the horizontal component of Earth's field B at that place is given by \[{{B}_{H}}=B\cos \delta \] At the magnetic equator, \[\delta =0{}^\circ ,\] \[{{B}_{H}}=B\cos 0{}^\circ =B\] At the magnetic poles, \[\delta =90{}^\circ ,\] \[{{B}_{H}}=B\cos 90{}^\circ =0\] Thus, the value of \[{{B}_{H}}\] is different at different places on the surface of the Earth. 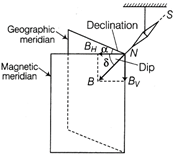 Horizontal component of Earth's field at a place Relations between elements of Earth's magnetic figure shows the three elements of Earth's magnetic field. If 8 is the angle of dip at any place, then the horizontal and vertical components of Earth's magnetic field B at that place will be \[{{B}_{H}}=B\cos \delta \] ?(i) and \[{{B}_{V}}=B\sin \delta \] \[\therefore \] \[\frac{{{B}_{V}}}{{{B}_{H}}}=\frac{B\sin \delta }{B\cos \delta }\] or \[\frac{{{B}_{V}}}{{{B}_{H}}}=\tan \delta \] ?(ii) Also, \[B_{H}^{2}+B_{V}^{2}={{B}^{2}}({{\cos }^{2}}\delta +{{\sin }^{2}}\delta )={{B}^{2}}\] or \[B=\sqrt{B_{H}^{2}+B_{V}^{2}}\] ?(iii) Eqs. (i), (ii) and (iii) are the different relations between the elements of Earth's magnetic field. By knowing the three elements, we can determine the magnitude and direction of the Earth's magnetic field at any place. (ii) Here, \[{{B}_{H}}=0.15\,G\] and \[{{B}_{V}}=0.30\,G\] \[\tan \delta =\frac{{{B}_{V}}}{{{B}_{H}}}=\frac{0.30}{0.15}=2\] \[\therefore \] \[\delta ={{\tan }^{-1}}2=63{}^\circ 4'\] and \[B=\sqrt{B_{H}^{2}+B_{V}^{2}}=\sqrt{{{(0.15)}^{2}}+{{(0.30)}^{^{2}}}}\] = 0.3354 G
Horizontal component of Earth's field at a place Relations between elements of Earth's magnetic figure shows the three elements of Earth's magnetic field. If 8 is the angle of dip at any place, then the horizontal and vertical components of Earth's magnetic field B at that place will be \[{{B}_{H}}=B\cos \delta \] ?(i) and \[{{B}_{V}}=B\sin \delta \] \[\therefore \] \[\frac{{{B}_{V}}}{{{B}_{H}}}=\frac{B\sin \delta }{B\cos \delta }\] or \[\frac{{{B}_{V}}}{{{B}_{H}}}=\tan \delta \] ?(ii) Also, \[B_{H}^{2}+B_{V}^{2}={{B}^{2}}({{\cos }^{2}}\delta +{{\sin }^{2}}\delta )={{B}^{2}}\] or \[B=\sqrt{B_{H}^{2}+B_{V}^{2}}\] ?(iii) Eqs. (i), (ii) and (iii) are the different relations between the elements of Earth's magnetic field. By knowing the three elements, we can determine the magnitude and direction of the Earth's magnetic field at any place. (ii) Here, \[{{B}_{H}}=0.15\,G\] and \[{{B}_{V}}=0.30\,G\] \[\tan \delta =\frac{{{B}_{V}}}{{{B}_{H}}}=\frac{0.30}{0.15}=2\] \[\therefore \] \[\delta ={{\tan }^{-1}}2=63{}^\circ 4'\] and \[B=\sqrt{B_{H}^{2}+B_{V}^{2}}=\sqrt{{{(0.15)}^{2}}+{{(0.30)}^{^{2}}}}\] = 0.3354 G
You need to login to perform this action.
You will be redirected in
3 sec
