| (i) What do you mean by the polarisation of light? Define law of Malus and then show that the intensity of light become half when ordinary light is incident on a polariser. |
| (ii) Two polarising sheets have their polarising direction parallel, so that the intensity of the transmitted light is maximum. |
| Through what angle must the either sheet be turned, if the intensity is to drop by one half? |
| Or |
| (i) Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. |
| Obtain the value of D in terms of \[\lambda \] such that the first minima on the screen falls at a distance D from the centre O. |
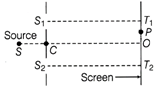 |
| (ii) Why are coherent sources required to create interference of light? |
Answer:
(i) Polarisation of light The ordinary light have electric field vectors in all possible directions in a plane perpendicular to the direction of propagation of light waves. When it is passed through a tourmaline crystal, then in transmitted light, only those electric field vectors are present which are parallel to the axis of crystal. 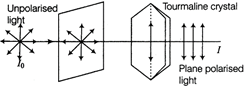 Polarisation of light Such light is called plane polarised light. The phenomena of restricting the electric vectors of light into particular direction is called polarisation of light. The tourmaline crystal acts as a polariser. Law of Malus When completely plane polarised light is incident on an analyser, the intensity of transmitted light is proportional to the square of the cosine of the angle \[(\theta )\] between the plane of polariser and analyser. \[I\propto {{\cos }^{2}}\theta ;\] \[I={{I}_{0}}{{\cos }^{2}}\theta \] where, \[{{I}_{0}}\] is the intensity of incident light. Let the intensity of the ordinary light be \[{{I}_{0}}\] and it is incident on a polariser. In ordinary light, electric vectors are in all possible directions and therefore intensity of transmitted light, \[I={{I}_{0}}{{({{\cos }^{2}}\theta )}_{av}}\] [average value of \[{{\cos }^{2}}\theta \]] \[{{({{\cos }^{2}}\theta )}_{av}}=\frac{1}{2\pi }\int_{0}^{2\pi }{{{\cos }^{2}}\theta d\theta }\] \[=\frac{1}{2\pi }\int_{0}^{2\pi }{\left[ \frac{1+\cos 2\theta }{2} \right]d\theta }\] \[=\frac{1}{4\pi }\left[ \theta +\frac{\sin 2\theta }{2} \right]_{0}^{2\pi }=\frac{1}{4\pi }\left[ 2\pi +\frac{\sin 4\pi }{2}-0 \right]\] \[=\frac{1}{4}\pi \times 2\pi \] \[\therefore {{({{\cos }^{2}}\theta )}_{av}}=\frac{1}{2}\Rightarrow I=\frac{{{I}_{0}}}{2}\] (ii) It is given that, \[I=\frac{{{I}_{0}}}{2}\] Using Malus law, \[I={{I}_{0}}{{\cos }^{2}}\theta \] \[\Rightarrow \] \[\frac{{{I}_{0}}}{2}={{I}_{0}}{{\cos }^{2}}\theta \] or \[{{\cos }^{2}}\theta =\pm \frac{1}{\sqrt{2}}\] \[\Rightarrow \] \[\theta =\pm 45{}^\circ ,\pm 135{}^\circ \] Or (i)
Polarisation of light Such light is called plane polarised light. The phenomena of restricting the electric vectors of light into particular direction is called polarisation of light. The tourmaline crystal acts as a polariser. Law of Malus When completely plane polarised light is incident on an analyser, the intensity of transmitted light is proportional to the square of the cosine of the angle \[(\theta )\] between the plane of polariser and analyser. \[I\propto {{\cos }^{2}}\theta ;\] \[I={{I}_{0}}{{\cos }^{2}}\theta \] where, \[{{I}_{0}}\] is the intensity of incident light. Let the intensity of the ordinary light be \[{{I}_{0}}\] and it is incident on a polariser. In ordinary light, electric vectors are in all possible directions and therefore intensity of transmitted light, \[I={{I}_{0}}{{({{\cos }^{2}}\theta )}_{av}}\] [average value of \[{{\cos }^{2}}\theta \]] \[{{({{\cos }^{2}}\theta )}_{av}}=\frac{1}{2\pi }\int_{0}^{2\pi }{{{\cos }^{2}}\theta d\theta }\] \[=\frac{1}{2\pi }\int_{0}^{2\pi }{\left[ \frac{1+\cos 2\theta }{2} \right]d\theta }\] \[=\frac{1}{4\pi }\left[ \theta +\frac{\sin 2\theta }{2} \right]_{0}^{2\pi }=\frac{1}{4\pi }\left[ 2\pi +\frac{\sin 4\pi }{2}-0 \right]\] \[=\frac{1}{4}\pi \times 2\pi \] \[\therefore {{({{\cos }^{2}}\theta )}_{av}}=\frac{1}{2}\Rightarrow I=\frac{{{I}_{0}}}{2}\] (ii) It is given that, \[I=\frac{{{I}_{0}}}{2}\] Using Malus law, \[I={{I}_{0}}{{\cos }^{2}}\theta \] \[\Rightarrow \] \[\frac{{{I}_{0}}}{2}={{I}_{0}}{{\cos }^{2}}\theta \] or \[{{\cos }^{2}}\theta =\pm \frac{1}{\sqrt{2}}\] \[\Rightarrow \] \[\theta =\pm 45{}^\circ ,\pm 135{}^\circ \] Or (i) 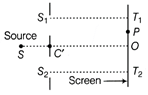 \[{{T}_{2}}P={{T}_{2}}O+OP=D+x\] and \[{{T}_{1}}P={{T}_{1}}O-OP=D-x\] \[{{S}_{1}}P=\sqrt{{{({{S}_{1}}{{T}_{1}})}^{2}}+{{(P{{T}_{1}})}^{2}}}=\sqrt{{{D}^{2}}+{{(D-x)}^{2}}}\] and \[{{S}_{2}}P=\sqrt{{{({{S}_{2}}{{T}_{2}})}^{2}}+{{({{T}_{2}}P)}^{2}}}=\sqrt{{{D}^{2}}+{{(D+x)}^{2}}}\] The minima will occur when \[{{S}_{2}}P-{{S}_{1}}P=(2n-1)\frac{\lambda }{2}\] i.e., \[{{[{{D}^{2}}+{{(D+x)}^{2}}]}^{1/2}}-[{{D}^{2}}+{{(D-{{x}^{2}}]}^{1/2}}=\frac{\lambda }{2}\] [for first minima n = 1] If \[x=D\] we can write \[{{[{{D}^{2}}+4{{D}^{2}}]}^{1/2}}-{{[{{D}^{2}}+0]}^{1/2}}=\frac{\lambda }{2}\] \[\Rightarrow \] \[{{[5{{D}^{2}}]}^{1/2}}-{{[{{D}^{2}}]}^{1/2}}=\frac{\lambda }{2}\] \[\Rightarrow \] \[\sqrt{5}D-D=\frac{\lambda }{2}\] \[\Rightarrow \] \[D(\sqrt{5}-1)=\lambda /2\] \[\Rightarrow \] \[D=\frac{\lambda }{2(\sqrt{5}-1)}\] Putting \[\sqrt{5}=2.236\] \[\Rightarrow \] \[\sqrt{5}-1=2.236-1=1.236\] \[D=\frac{\lambda }{2(1.236)}=0.404\lambda \] (ii) To observe interference fringe pattern, there is need to have coherent sources of light which can produce light of constant phase difference.
\[{{T}_{2}}P={{T}_{2}}O+OP=D+x\] and \[{{T}_{1}}P={{T}_{1}}O-OP=D-x\] \[{{S}_{1}}P=\sqrt{{{({{S}_{1}}{{T}_{1}})}^{2}}+{{(P{{T}_{1}})}^{2}}}=\sqrt{{{D}^{2}}+{{(D-x)}^{2}}}\] and \[{{S}_{2}}P=\sqrt{{{({{S}_{2}}{{T}_{2}})}^{2}}+{{({{T}_{2}}P)}^{2}}}=\sqrt{{{D}^{2}}+{{(D+x)}^{2}}}\] The minima will occur when \[{{S}_{2}}P-{{S}_{1}}P=(2n-1)\frac{\lambda }{2}\] i.e., \[{{[{{D}^{2}}+{{(D+x)}^{2}}]}^{1/2}}-[{{D}^{2}}+{{(D-{{x}^{2}}]}^{1/2}}=\frac{\lambda }{2}\] [for first minima n = 1] If \[x=D\] we can write \[{{[{{D}^{2}}+4{{D}^{2}}]}^{1/2}}-{{[{{D}^{2}}+0]}^{1/2}}=\frac{\lambda }{2}\] \[\Rightarrow \] \[{{[5{{D}^{2}}]}^{1/2}}-{{[{{D}^{2}}]}^{1/2}}=\frac{\lambda }{2}\] \[\Rightarrow \] \[\sqrt{5}D-D=\frac{\lambda }{2}\] \[\Rightarrow \] \[D(\sqrt{5}-1)=\lambda /2\] \[\Rightarrow \] \[D=\frac{\lambda }{2(\sqrt{5}-1)}\] Putting \[\sqrt{5}=2.236\] \[\Rightarrow \] \[\sqrt{5}-1=2.236-1=1.236\] \[D=\frac{\lambda }{2(1.236)}=0.404\lambda \] (ii) To observe interference fringe pattern, there is need to have coherent sources of light which can produce light of constant phase difference.
You need to login to perform this action.
You will be redirected in
3 sec
