question_answer

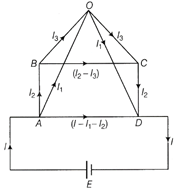
Eight identical resistances r each are connected along edges of pyramid have square base AB CD as shown in figure. Calculate the equivalent resistance between A and D. Or A cylindrical tube of length L has inner radius while outer b as shown in Fig. 9.19 (a). What is the resistance of the tube between (i) its ends (ii) its inner and outer surfaces? [The resistivity of its material is p.]

Answer:

Equivalent resistance \[=\frac{8}{15}r\] Or (i) \[\frac{\rho I}{\pi ({{b}^{2}}-{{a}^{2}})}\]  (ii) \[\frac{\rho }{2\pi I}In\left( \frac{b}{a} \right)\] We connect a cell of emf E across A and D. Let the distribution of current S in the various arms be as shown in figure. According to Kirchhoff?s second rule in the closed circuit BOCB. \[{{I}_{3}}r+{{I}_{3}}r-({{I}_{2}}-{{I}_{3}})r=0\]             or         \[3{{I}_{3}}={{I}_{2}}\]             or         \[{{I}_{3}}={{I}_{2}}/2\]                                 ?(i) In the closed circuit AODA,             \[{{I}_{1}}r+{{I}_{1}}r-(I-{{I}_{1}}-{{I}_{2}})r=0\] or         \[3{{I}_{1}}+{{I}_{2}}=I\]                              ?(ii) In the closed circuit ABCDA, \[{{I}_{2}}r+({{I}_{2}}-{{I}_{3}})r+{{I}_{2}}r-(I-{{I}_{1}}-{{I}_{2}})r=0\] or \[I={{I}_{1}}+4{{I}_{2}}-{{I}_{3}}={{I}_{1}}+4{{I}_{2}}-\frac{{{I}_{2}}}{3}={{I}_{1}}+\frac{11}{3}{{I}_{2}}\]                                                          ?(iii) From Eqs. (ii) and (iii), we have             \[3{{I}_{1}}+{{I}_{2}}={{I}_{1}}+\frac{11}{3}{{I}_{2}}\] or         \[{{I}_{2}}=\frac{6}{8}{{I}_{1}}=\frac{3}{4}{{I}_{1}}\] From Eq. (ii),\[I=3{{I}_{1}}+\frac{3}{4}{{I}_{1}}=\frac{15}{4}{{i}_{1}}\] In the closed circuit ADEA,             \[E=(I-{{I}_{1}}-{{I}_{2}})r\]             \[=\left( \frac{15}{4}{{I}_{1}}-{{I}_{1}}-\frac{3}{4}{{I}_{1}} \right)=2{{I}_{1}}r\] If R is the resistance of network between A and D then             \[E=IR=\frac{15}{4}{{I}_{1}}R\] From Eqs. (iv) and (v), we have             \[\frac{15}{4}{{I}_{1}}R=2{{I}_{1}}r\]or\[R=\frac{8}{15}r\] Or (i) In a case of electrical conduction, field at a point inside a conductor is given by, \[J=\sigma \,\,E,\,\,i.e.\,E=\rho J[as\sigma =(1/\rho )]\]       ?(i) As here the current and field are along the axis of the tube, consider the tube to be made up of large number of co-axial annular discs and considering a disc of thickness dx at distance x from one end as shown in Fig. (i), we have \[E=-\frac{dv}{dx}\text{and}\,\,\text{J=}\frac{1}{\pi ({{b}^{2}}-{{\text{a}}^{2}})}[as\,S=\pi ({{b}^{2}}-{{a}^{2}})]\] So Eq. (i) reduce to:             \[-\frac{dV}{dx}=\rho \frac{I}{\pi ({{b}^{2}}-{{a}^{2}})},\] i.e.        \[-\int_{{{V}_{1}}}^{{{V}_{2}}}{dV\int_{0}^{L}{\frac{\rho \,\,Idx}{\pi \,\,({{b}^{2}}-{{a}^{2}})}}}\] or,        \[V=({{V}_{1}}-{{V}_{2}})=\frac{\rho \,\,LI}{\pi ({{b}^{2}}-{{a}^{2}})}\] so,        \[R=\frac{V}{I}=\frac{\rho L}{\pi ({{b}^{2}}-{{a}^{2}})}\] (ii) As here the field is radial, consider the tube to be made up of large number of concentric cylindrical shells and considering as shell to radius r and thickness dr as shown in Fig. (b), we have 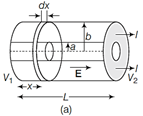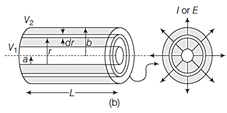\[E=-\frac{dV}{dr}\]and\[J=\frac{I}{2\pi rL}\]     \[[as\,\,here\,\,S=2\,\,\pi rL]\] So, Eq. (i) for this case becomes,                         \[-\frac{dV}{dr}=\frac{\rho i}{2\pi \,\,rL},i.e.\,\,\,\,-\int_{{{V}_{1}}}^{{{V}_{2}}}{dV=\int_{a}^{b}{\frac{\rho Idr}{2\pi \,\,rL}}}\]             or         \[V=({{V}_{1}}-{{V}_{2}})=\frac{\rho I}{2\pi \,\,L}{{\log }_{e}}\left[ \frac{b}{\text{a}} \right]\]             So        \[R=\frac{V}{I}=\frac{\rho }{2\pi L}{{\log }_{e}}\left[ \frac{b}{\text{a}} \right]\]