question_answer

(i) Consider two coherent sources \[{{S}_{1}}\] and \[{{S}_{2}}\] producing monochromatic waves to produce interference pattern. Let the displacement of the wave produced by  \[{{S}_{1}}\] be given by  \[{{Y}_{1}}=a\cos \,\omega t\] and the displacement by \[{{S}_{2}}\] be \[{{Y}_{2}}=a\cos (\omega t+\phi )\]

Find out an expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be \[I=4{{a}^{2}}{{\cos }^{2}}\frac{\phi }{2}\] Hence, establish the conditions for constructive and destructive interference.

(ii) What is the effect on the interference fringes in Young's double slit experiment when (i) the width of the source slit is increased; (ii) the monochromatic source is replaced by a source of white light?

OR

Figure shows a modified Young's double slit experimental set up. where \[S{{S}_{2}}-S{{S}_{1}}=\frac{\lambda }{4},\] then

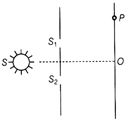
(i) state the condition for constructive and destructive interference.

(ii) define fringe width and obtain an expression for the fringe width

(iii) locate the position of the central fringe.

    

Answer:

(i) Given the displacements of two coherent sources \[{{y}_{1}}=a\,\cos \,\,\omega \,t\] or \[{{y}_{2}}=a\,\cos \,\,(\omega \,t+\phi )\] By principle of superposition, resultant displacement, \[y={{y}_{1}}+{{y}_{2}}=a\,\cos \,\,\omega \,t+a\cos \,(\omega \,t+\phi )\] Or \[y=a\,\cos \,\,\omega \,t+a\cos \,\omega \,t\cos \phi =a\sin \omega \,t\sin \phi \]  \[y=a\,(1+\cos \phi )\cdot \cos \,\omega \,t+(-\,a\sin \phi )\sin \omega \,t\] Let        \[a\,(1+cos\phi )=A\cos \phi \]                 ? (i) And      \[a\sin \phi =A\sin \theta \]                                   ? (ii) \[\therefore \]      \[y=A\cos \theta \cos \omega \,t-A\sin \theta \sin \omega \,t\] \[\Rightarrow \]   \[y=A\cos \,(\omega \,t+\theta )\]             ? (iii) Squaring and adding Eqn. (i) and (ii), we get \[{{(A\cos \theta )}^{2}}+{{(A\sin \theta )}^{2}}={{a}^{2}}{{(1+\cos \phi )}^{2}}+{{(a\sin \phi )}^{2}}\] \[\Rightarrow \]   \[{{A}^{2}}({{\cos }^{2}}\theta +{{\sin }^{2}}\theta )\]             \[={{a}^{2}}(1+{{\cos }^{2}}\phi +2\cos \phi )+{{a}^{2}}{{\sin }^{2}}\phi \] \[\Rightarrow \]   \[{{A}^{2}}\times 1={{a}^{2}}+{{a}^{2}}+2{{a}^{2}}\cos \phi \] \[\Rightarrow \]   \[{{A}^{2}}=2{{a}^{2}}(1+\cos \phi )\] \[\Rightarrow \]   \[{{A}^{2}}=2{{a}^{2}}\left( 2{{\cos }^{2}}\frac{\phi }{2} \right)=4{{a}^{2}}{{\cos }^{2}}\left( \frac{\phi }{2} \right)\] If I is the resultant intensity, then \[\Rightarrow \]   \[I=4{{a}^{2}}{{\cos }^{2}}\frac{\phi }{2}\]              \[[\because I\propto {{A}^{2}}]\] Condition for bright fringe or constructive interference \[\cos \left( \frac{\phi }{2} \right)=\pm \,1,\] then \[I={{I}_{0}}=4{{a}^{2}}\Rightarrow \frac{\phi }{2}=n\pi \] or \[\phi =2n\pi \]             Where, \[n=0,1,2,3,......,\]             Also, path difference \[\Delta \text{x=}\frac{\lambda }{2\pi }\times \] phase difference             \[\Rightarrow \]   \[\Delta \text{x=}\frac{\lambda }{2\pi }\times 2n\pi \]             Path difference, \[\Delta \text{x}\,\,\text{=}\,\,n\lambda \] Bright fringe is obtained when path difference of interfering wave is \[n\lambda \] and phase difference is \[2n\pi .\] Condition of dark fringe or destructive interference \[I=0\]             \[\Rightarrow \] \[\cos \frac{\phi }{2}=0\Rightarrow \cos \frac{\phi }{2}=0=\cos \,(2n+1)\frac{\pi }{2}\]             \[\Rightarrow \]   \[\frac{\phi }{2}=(2n+1)\frac{\pi }{2},\] where \[n=0,1,2\]             \[\Rightarrow \] \[\phi =(2n+1)\pi ,\] Where, \[n=0,1,2\]             Path difference, \[\Delta \text{x=}\frac{\lambda }{2\pi }\times \phi =\frac{\lambda }{2\pi }\times (2n+1)\,\pi \]                         \[\Delta \text{x=(2n+1)}\lambda /2\]             Path difference, \[\Delta \text{x}\,\,\text{=}\,\,\text{(2n}\,\text{+1)}\lambda /2\] Dark fringes are obtained when interfering wave has path difference in odd multiple of \[\lambda /2\] and phase difference is odd multiple of \[\pi .\] (ii) For fringes to be seen, \[\frac{s}{S}\le \frac{\lambda }{d}\] Condition should be satisfied. where, s = size of the source and S = distance of the source from the plane of two slits. As the source slit width increases, the fringe pattern get less and less sharp. When the source slit is so wide, the above condition does not satisfied and the interference pattern disappears. The interference pattern due to different colour component of white light overlaps. The control bright fringes for different colours are at the same position. Therefore, the centre fringes are white. And on the either side of the central fringe, i.e. central maxima, coloured bands will appear. The fringe closed on either side of central white fringe is red and the farthest will be blue. After a few fringes, no clear fringes pattern is seen. Or (i) Initial path difference between \[{{S}_{1}}\] and \[{{S}_{2}},\] \[{{\Delta }_{0}}=S{{S}_{2}}-S{{S}_{1}}=\frac{\lambda }{4}\] 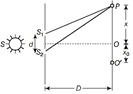Path difference between disturbances from \[{{S}_{1}}\]and \[{{S}_{2}}\] at point P, \[\Delta =\frac{\text{x}d}{D}\] Total path difference between the two disturbances at P, \[{{\Delta }_{T}}={{\Delta }_{0}}+\Delta =\frac{\lambda }{4}+\frac{\text{x}d}{D}\] For constructive interference             \[{{\Delta }_{T}}=\left( \frac{\lambda }{4}+\frac{\text{x}d}{D} \right)=n\lambda ;\] where\[n=0,1,2,...\] Or         \[\frac{{{\text{x}}_{n}}d}{D}=\left( n-\frac{1}{4} \right)\lambda \] For destructive interference, \[{{\Delta }_{T}}=\left( \frac{\lambda }{4}+\frac{\text{x}d}{D} \right)=(2n-1)\frac{\lambda }{2}\] Or         \[\frac{X{{'}_{n}}d}{D}=\left( 2n-1-\frac{1}{2} \right)\frac{\lambda }{2}\] \[\frac{X{{'}_{n}}d}{D}=\left( 2n-\frac{3}{2} \right)\frac{\lambda }{2}\]              ? (ii) (ii) Fringe width Distance between two adjacent bright (or dark) fringes is called the fringe width. it is denoted by \[\beta .\] Fringe width, \[\beta ={{x}_{n+1}}-{{\text{x}}_{n}}=\frac{\lambda D}{d}\] The position \[{{\text{x}}_{\text{0}}}\] of central fringe is obtained by putting \[n=0\] in Eq. (i), we get \[\therefore \]      \[{{\text{x}}_{0}}=-\frac{\lambda D}{4d}\] The negative sign shows that the central fringe is obtained at point O' below the (central) point O.