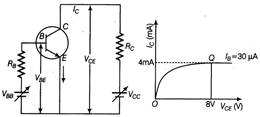
 Given that the input impedance of the transistor is very small and \[{{V}_{CC}}={{V}_{BB}}=16V,\] find the voltage gain and power gain of circuit making appropriate assumptions.
Given that the input impedance of the transistor is very small and \[{{V}_{CC}}={{V}_{BB}}=16V,\] find the voltage gain and power gain of circuit making appropriate assumptions.
Answer:
For the output characteristic at Q \[{{V}_{CC}}={{I}_{C}}{{R}_{C}}+{{V}_{CE}}\] \[{{R}_{C}}=\frac{{{V}_{CC}}-{{V}_{CE}}}{{{I}_{C}}}=\frac{16-8}{4\times {{10}^{-3}}}\] \[=\frac{8000}{4}=2k\Omega \] Using the relation \[{{V}_{BB}}={{I}_{B}}{{R}_{B}}+{{V}_{BE}}\] \[{{R}_{B}}=\frac{{{V}_{BB}}-{{V}_{BE}}}{{{I}_{B}}}\] \[=\frac{16-0.7}{30\times {{10}^{-6}}}=510\times {{10}^{3}}\Omega =510k\Omega \] \[\beta =\frac{{{I}_{C}}}{{{I}_{B}}}=\frac{4\times {{10}^{-3}}}{30\times {{10}^{-6}}}\approx 133\] Voltage gain \[=\beta \times \frac{{{R}_{C}}}{{{R}_{B}}}=\frac{133\times 2\times {{10}^{3}}}{510\times {{10}^{3}}}=0.52\] Power gain \[=\beta \times \]Voltage gain \[=133\times 0.52=69.36\] Given, \[{{V}_{BE}}=0.7V,\] \[{{V}_{CC}}={{V}_{BB}}=16V\] \[{{V}_{CE}}=8V\] (from graph) \[{{I}_{C}}=4mA=4\times {{10}^{-3}}A\] \[{{I}_{B}}=30\mu A=30\times {{10}^{-6}}A\]
You need to login to perform this action.
You will be redirected in
3 sec
