question_answer

Two spheres carrying charges \[1.5\mu C\] and \[2.5\mu C\] are located 30 cm apart. Find the potential and electric field

(i) at mid-point of the line joining the two charges.

(ii) at a point 10 cm from this mid-point in a plane normal to the line passing through the mid-point.

Hence, calculate the angle \[(\alpha )\] subtended by the resultant intensity of electric field in case (ii).

Or

(i) Deduce the expression for the energy density stored in a charged capacitor.

(ii) Show that the effective capacitance C, of a series combination, of three capacitors \[{{C}_{1}},{{C}_{2}}\] and \[{{C}_{3}}\] is given by

\[C=\frac{{{C}_{1}}{{C}_{2}}{{C}_{3}}}{({{C}_{1}}{{C}_{2}}+{{C}_{2}}{{C}_{3}}+{{C}_{3}}{{C}_{1}})}\]

Answer:

            (i) Given, \[{{q}_{1}}=1.5\mu C=1.5\times {{10}^{-6}}C,\]             \[{{q}_{2}}=2.5\mu C,=2.5\times {{10}^{-6}}C\] Distance between the two spheres = 30 cm = 0.3 m 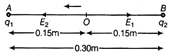For the mid-point O, \[{{r}_{1}}={{r}_{2}}=\frac{0.30}{2}=0.15m\] Therefore, potential, \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\left[ \frac{{{q}_{_{1}}}}{{{r}_{1}}}+\frac{{{q}_{2}}}{{{r}_{2}}} \right]\]             \[=\frac{9\times {{10}^{9}}}{0.15}(1.5\times {{10}^{-6}}+2.5\times {{10}^{-6}})\] \[=\frac{9\times {{10}^{9}}\times 4.0\times {{10}^{-6}}}{0.15}\]                         \[=2.4\times {{10}^{5}}\,V\]             Electric field at O, \[E={{E}_{2}}-{{E}_{1}}\]                                     \[=\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{{{q}_{2}}-{{q}_{1}}}{{{r}^{2}}} \right)\]             \[=\frac{9\times {{10}^{9}}\times (2.5\times {{10}^{-6}}-1.5\times {{10}^{-6}})}{{{(0.15)}^{2}}}\]             \[=4.0\times {{10}^{5}}V/m\]  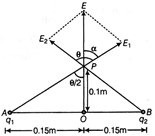           Consider point P in a plane normal to the line passing through the mid-point, where OP = 10 cm = 0.1 m. Using pythagoras theorem, \[PA=PB=\sqrt{{{(0.15)}^{2}}+{{(0.10)}^{2}}}=0.18m\] Therefore, potential at point P,             \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{1}}}{PA}+\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{2}}}{PB}\]             \[=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{({{q}_{1}}+{{q}_{2}})}{PA}\]             \[=\frac{9\times {{10}^{9}}}{(0.18)}(1.5\times {{10}^{-6}}+2.5\times {{10}^{-6}})\]             \[=2\times {{10}^{5}}V\] Similarly, electric field at point P, due to \[{{q}_{1}},\]             \[{{E}_{1}}=\frac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}{{(PA)}^{2}}}\]             \[=\frac{9\times {{10}^{9}}\times 1.5\times {{10}^{-6}}}{{{(0.18)}^{2}}}\]             \[=0.42\times {{10}^{6}}V{{m}^{-1}},\]  along AP produced. Electric field at point P due to \[{{q}_{2}},\] \[{{E}_{2}}=\frac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}{{(PB)}^{2}}}\]             \[=\frac{9\times {{10}^{9}}\times 2.5\times {{10}^{-6}}}{{{(0.18)}^{2}}}\] \[=0.69\times {{10}^{6}}V{{m}^{-1}},\] along BP produced. Also, \[\cos \left( \frac{\theta }{2} \right)=\frac{PO}{AP}=\frac{0.10}{0.18}=\frac{5}{9}=0.5556\] \[\Rightarrow \]   \[\frac{\theta }{2}={{\cos }^{-1}}(0.5556)=56.25{}^\circ \] \[\Rightarrow \]   \[\theta =112.5{}^\circ \] \[\therefore \] Resultant intensity at P,             \[E=\sqrt{E_{1}^{2}+E_{2}^{2}+2{{E}_{1}}{{E}_{2}}\cos \theta }\]             \[=6.58\times {{10}^{5}}V{{m}^{-1}}\] Let \[\alpha \] be the angle which the resultant intensity E makes with \[{{E}_{1}}.\] \[\therefore \]      \[\tan \alpha =\frac{{{E}_{2}}\sin \theta }{{{E}_{1}}+{{E}_{2}}\sin \theta }\]             \[=\frac{0.69\times {{10}^{6}}\times 0.9239}{0.42\times {{10}^{6}}+0.69\times {{10}^{6}}(-0.38)}\] \[\Rightarrow \]   \[\tan \alpha =\frac{0.698}{0.16}=4.3\]             \[\alpha ={{\tan }^{-1}}(4.3)=76.9{}^\circ \] (i) We know that, \[q=CV\Rightarrow V=q/C\] \[\therefore \] \[dW=Vdq=\frac{q}{C}dq\] where, q = instantaneous charge, C = instantaneous capacitance and       V= instantaneous voltage. \[\therefore \] Total work done in storing charge from 0 to q is given by             \[W=\int_{0}^{q}{\frac{q}{C}dq=\frac{{{q}^{2}}}{2C}}\] (ii) In series combination of capacitors, same charge lie on each capacitor for any value of capacitances. 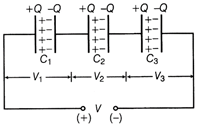Capacitors in series combination Also, potential difference across the combination is equal to the algebraic sum of potential differences across each capacitor, i.e. \[V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}\]                                             ?(i) where, \[{{V}_{1}},{{V}_{2}},{{V}_{3}}\] and V are the potential differences across \[{{C}_{1}},{{C}_{2}},{{C}_{3}}\] and equivalent capacitor, respectively. \[\therefore \]      \[q={{C}_{1}}{{V}_{1}}\Rightarrow {{V}_{1}}=\frac{q}{{{C}_{1}}}\] Similarly, \[{{v}_{2}}=\frac{q}{{{C}_{2}}}\] and \[{{v}_{3}}=\frac{q}{{{C}_{3}}}\]   [from Eq.(i)] \[\therefore \] Total potential difference,             \[V=\frac{q}{{{C}_{1}}}+\frac{q}{{{C}_{2}}}+\frac{q}{{{C}_{3}}}\]             \[\frac{V}{q}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}\]             \[\frac{1}{C}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}\] [\[\because \frac{V}{q}=\frac{1}{C},\] where C is equivalent capacitance of combination] or \[\frac{1}{C}=\frac{{{C}_{2}}{{C}_{3}}+{{C}_{3}}{{C}_{1}}+{{C}_{1}}{{C}_{2}}}{{{C}_{1}}{{C}_{2}}{{C}_{3}}}\] \[\Rightarrow \]   \[C=\frac{{{C}_{1}}{{C}_{2}}{{C}_{3}}}{{{C}_{1}}{{C}_{2}}+{{C}_{2}}{{C}_{3}}+{{C}_{3}}{{C}_{1}}}\]