question_answer

A 50 MHz sky wave takes 4.04 ms to reach a receiver via re-transmission from a satellite 600 km above Earth's surface. Assuming re-transmission time by satellite negligible, find the distance between source and receiver. If communication between the two was to be done by Line of Sight (LOS) method, what should size and placement of receiving and transmitting antennas be?

Answer:

            Let the receiver be at point A and source be at B, 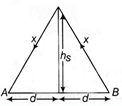Re-transmission from a satellite Given, velocity of waves \[3\times {{10}^{8}}m/s\] Time to reach a receiver \[=4.04\text{ }ms=4.04\times {{10}^{-3}}s\] Let the height of satellite is, \[{{h}_{s}}=600km\] Radius of Earth = 6400 km Size of transmitting antenna = hf We know that, \[\frac{\text{Distance travelled by wave}}{\text{Time}}\text{=Velocity}\,\,\text{of}\,\,\text{waves}\] \[\Rightarrow \]   \[\frac{2x}{4.04\times {{10}^{-3}}}=3\times {{10}^{8}}\] or         \[x=\frac{3\times {{10}^{8}}\times 4.04\times {{10}^{-3}}}{2}\] \[=6.06\times {{10}^{5}}=606km\] Using Pythagoras theorem,             \[{{d}^{2}}={{x}^{2}}-h_{s}^{2}={{(606)}^{2}}-{{(600)}^{2}}=7236\] or         d = 85.06 km So, the distance between source and receiver \[=2d=2\times 85.06=170\,km~\] The maximum distance covered on ground from the transmitter by emitted EM waves,             \[d=\sqrt{2R{{h}_{T}}}\]or \[{{d}^{2}}/2R={{h}_{T}}\] or size of antenna,             \[{{h}_{T}}=\frac{7236}{2\times 6400}=0.565\,km=565m\]