question_answer

(i) Draw the ray diagram for the formation of image of an object by a convex mirror and use it (along with the sign convention) to derive mirror formula.

(ii) Use the mirror formula to show that an object kept between the pole and focus of a concave mirror then the image appears to be formed behind the mirror.

Or

With the help of a ray diagram, show the formation of image of a point object by refraction of light at a spherical surface separating two media of refractive indices \[{{n}_{1}}\] and \[{{n}_{2}}\] \[({{n}_{2}}>{{n}_{1}}),\] respectively. Using this diagram, derive the relation

\[\frac{{{n}_{2}}}{v}-\frac{{{n}_{1}}}{u}=\frac{{{n}^{2}}-{{n}_{1}}}{R}\]

Write the sign conventions used.

An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change, if the lens is reversed?

Answer:

            (i) Let the convex mirror forms virtual, erect and diminished image A?B? on the other side of mirror of an object AB as shown in the figure. 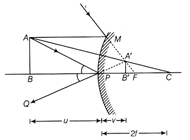                        Let        \[PC=+2f=R\]                         \[PB'=+v\]                         \[PB=-u\] \[\because \Delta \,A'B'C\] is similar to \[\Delta \,ABC\] \[\Rightarrow \]   \[\frac{A'B}{AB}=\frac{CB'}{CB}=\frac{PC-PB'}{PC+PB}=\frac{R-v}{R-u}\]     ?(i) Also \[\Delta \,A'B'P\sim \Delta \,ABP\] \[\Rightarrow \] \[\frac{A'B}{AB}=\frac{PB'}{PB}=\frac{v}{-u}\]                    ? (ii) From Eqs. (i) and (ii), we get \[\frac{R-v}{R-u}=-\frac{v}{u}\] or         \[uR-uv=-vR+uv\]             \[2uv=uR+vR\] On dividing by uvR, we get             \[\frac{2}{R}=\frac{1}{v}+\frac{1}{u}\] \[\because \]       R = 2f or         \[\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\] This is the required expression for mirror formula. (ii) For concave mirror, f < 0 Object distance, u < 0 But \[|f|\,>\,|u|\,>0\] By mirror formula, we have \[\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\] or         \[\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\] \[\because \]       \[f=-|f|\]             \[u=-|u|\]             \[\frac{1}{v}=\frac{1}{-|f|}+\frac{1}{|u|}\] \[\Rightarrow \]   \[\frac{1}{v}=\frac{1}{|u|}-\frac{1}{|f|}\] \[\Rightarrow \]   \[(v>0)\] But       \[|u|<|f|\] \[\Rightarrow \]   \[\frac{1}{|u|}>\frac{1}{|f|}\] \[\Rightarrow \]   \[\frac{1}{|u|}-\frac{1}{|f|}>0\] \[\Rightarrow \]   \[\frac{1}{v}>0\] Hence, the image form on the other side of mirror as v is positive. Or Let a point object O is placed at a distance, u from the pole in a medium of refractive index, \[{{n}_{1}}\] outside the spherical refracting surface of radius of curvature, R. Its real image, I is formed at a distance, v in denser medium of refractive index, \[{{n}_{2}}.\] Angle of incidence is / and angle of refraction is r. Real image of a point object Draw a normal AN on principal axis. Let        \[\angle AOC=\alpha ,\] \[\angle AIC=\beta ,\] \[\angle ACO=\gamma \] For \[\Delta \,AOC,\] i is the exterior angle             \[i=\alpha +\gamma \] For \[\Delta \,AIC,\] \[\gamma \] is the exterior angle \[\therefore \]      \[\gamma =r+\beta \] or \[r=\gamma -\beta \]                   ?(ii) According to the Snell?s law, \[\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{\sin \,i}{\sin \,r}\] when angles i and r are very small, then \[\sin i\approx i\] and \[\sin \,r\approx r\] \[\therefore \]      \[\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{i}{r}\] or         \[{{n}_{1}}i={{n}_{2}}r\] Substituting the values of i and r from Eqs. (i) and (ii), we get             \[{{n}_{1}}(\alpha +\gamma )={{n}_{2}}(\gamma -\beta )\]                   ?(iii) If the aperture of the spherical surface is small, then angles \[\alpha ,\,\beta \] and \[\gamma \] will be small and point N will lie near to pole P. Then,             \[\alpha =\tan \alpha =\frac{AN}{ON}\approx \frac{AN}{OP}=\frac{AN}{(-u)}\]             \[\beta =\tan \beta =\frac{AN}{IN}\approx \frac{AN}{IP}=\frac{AN}{V}\]             \[\gamma =\tan \gamma =\frac{AN}{CN}\approx \frac{AN}{CP}=\frac{AN}{R}\] Substituting the values of \[\alpha ,\,\beta \] and \[\gamma \] in Eq. (iii), we get \[{{n}_{1}}\times AN\left[ \frac{1}{(-u)}+\frac{1}{R} \right]={{n}_{2}}\times AN\left[ \frac{1}{R}-\frac{1}{v} \right]\]             \[-\frac{{{n}_{1}}}{u}+\frac{{{n}_{1}}}{R}=\frac{{{n}_{2}}}{R}-\frac{{{n}_{2}}}{v}\] \[\Rightarrow \]   \[\frac{{{n}_{2}}}{v}-\frac{{{n}_{1}}}{u}=\frac{{{n}_{2}}-{{n}_{1}}}{R}\] Sign convention The distance measured from pole in the direction of propagation of light rays are taken positive and distances measured from pole in opposite to the direction of propagation of light rays are taken negative. Heights measured above the principal axis are take positive and below the principal axis as negative. No, it is because in lens maker?s formula, \[\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\] \[=(\mu -1)\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\] \[=(\mu -1)\left( \frac{1}{{{R}_{2}}}-\frac{1}{{{R}_{1}}} \right)\] i.e. on reversing the lens, values and sings of \[{{R}_{1}}\] and \[{{R}_{2}}\] get reversed. Thus, for a given position of object \[(\mu ),\] position of image (v) remains unchanged.