question_answer

A cell of emf 'E' and internal resistance r is connected across a variable resistor R. Plot a graph showing the variation of terminal potential V with resistance R. Predict from the graph, the condition under which V becomes equal to E.

OR

Apply Kirchhoff's laws to the loops ACBPA and ACBQA to write the expressions for the currents \[{{I}_{1}},{{I}_{2}}\] and \[{{I}_{3}}\] in the network given below.

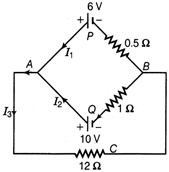
Circuit diagram of loops

 

Answer:

            According to given conditions in the question, the circuit diagram can be given as, 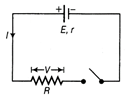From the above diagram,             \[V=IR=\frac{E}{R+r}\cdot R=\frac{E}{\frac{R+r}{R}}=\frac{E}{1+\frac{r}{R}}\]             \[\therefore \]      \[V=\frac{E}{1+\frac{r}{R}}\] When    R = 0, V = 0 When    R = r, \[V=\frac{E}{2}\] When    \[R=\infty ,\] V = E The plot showing variation of V vs R is given below. 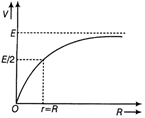From the above graph, it is clear that V becomes equal to E when \[R\to \infty \] Or Apply Kirchhoff's 1st law at point A of the circuit             \[{{I}_{3}}={{I}_{1}}+{{I}_{2}}\]                              ?(i) Applying Kirchhoff's IInd law to loop ACBPA \[-12{{I}_{3}}-0.5{{I}_{1}}+6=0\] or \[0.5{{I}_{1}}+12{{I}_{3}}=6\] ?(ii) Applying Kirchhoff's IInd law to loop ACBQA             \[-12{{I}_{3}}-{{I}_{2}}+10=0\] or,        \[{{I}_{2}}+12{{I}_{3}}=10\] The Eqs. (ii) and (iii) are required expressions.