Answer:
According to the question, 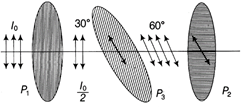 Intensity through \[{{P}_{1}},{{I}_{1}}=\frac{{{I}_{0}}}{2}\] Intensity through \[{{P}_{3}},\] \[{{I}_{3}}={{I}_{1}}{{\cos }^{2}}30{}^\circ \] (from malus? law, \[I={{I}_{0}}{{\cos }^{2}}\theta \]) \[=\frac{{{I}_{0}}}{2}{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}\] \[\left( \because \cos 30{}^\circ =\frac{\sqrt{3}}{2} \right)\] Therefore, intensity through \[{{P}_{2}},\] \[{{I}_{2}}={{I}_{3}}{{\cos }^{2}}60{}^\circ \] \[=\frac{{{I}_{0}}}{2}.\frac{3}{4}.{{\left( \frac{1}{2} \right)}^{2}}\] \[(\because v\cos \,60{}^\circ =1/2)\] \[=\frac{3}{32}{{I}_{0}}\]
Intensity through \[{{P}_{1}},{{I}_{1}}=\frac{{{I}_{0}}}{2}\] Intensity through \[{{P}_{3}},\] \[{{I}_{3}}={{I}_{1}}{{\cos }^{2}}30{}^\circ \] (from malus? law, \[I={{I}_{0}}{{\cos }^{2}}\theta \]) \[=\frac{{{I}_{0}}}{2}{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}\] \[\left( \because \cos 30{}^\circ =\frac{\sqrt{3}}{2} \right)\] Therefore, intensity through \[{{P}_{2}},\] \[{{I}_{2}}={{I}_{3}}{{\cos }^{2}}60{}^\circ \] \[=\frac{{{I}_{0}}}{2}.\frac{3}{4}.{{\left( \frac{1}{2} \right)}^{2}}\] \[(\because v\cos \,60{}^\circ =1/2)\] \[=\frac{3}{32}{{I}_{0}}\]
You need to login to perform this action.
You will be redirected in
3 sec
