question_answer

A conducting rod PQ of length l, connected to a resistor R, is moved at a uniform speed v, normal to a uniform magnetic field B as shown in the figure.

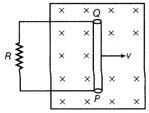
(i) Deduce the expression for the emf induced in the conductor.

(ii) Find the force required to move the rod in the magnetic field.

(iii) Mark the direction of induced current in the conductor.

Answer:

(i) Let the lengths of horizontal arms of circuit be \[{{x}_{1}}\] and \[{{x}_{2}}\] at instants, \[{{t}_{1}}\] and \[{{t}_{2}},\] respectively. 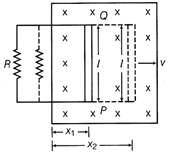\[\therefore \] Area of loop inside the magnetic field, \[{{A}_{1}}=l{{x}_{1}},\] \[{{A}_{2}}=l{{x}_{2}}\] \[\therefore \]      \[\Delta \,A={{A}_{2}}-{{A}_{1}}=l({{x}_{2}}-{{x}_{1}})=l\,\Delta \,x\]             \[\Delta \,\phi =B\Delta \,A=Bl\Delta x\] \[\therefore \]    \[\frac{\Delta \,\phi }{\Delta \,t}=Bl\frac{\Delta \,x}{\Delta \,t}=Blv\] By Faraday's law of induced emf (in magnitude). \[e=\frac{\Delta \,\phi }{\Delta \,t}=vBl\] \[\therefore \]      \[e=vBl\] (ii) Current (I) in the loop, Force required must be equal to magnetic force acting on conductor PQ in the opposite directions. \[\therefore \]      \[F=IBl\sin 90{}^\circ =(vBl/R)Bl\]                         \[F=\frac{v{{B}^{2}}{{l}^{2}}}{R}\] (iii) By Fleming's right hand rule, the direction of flow of current is along anti-clockwise direction.