question_answer

(i) Explain with the help of diagram, how plane polarised light is obtained by scattering?

(ii) Between two polaroids placed in crossesd position, a third polaroid is introduced. The axis of the third polaroid makes an angle of \[30{}^\circ \] with the axis of the crossed polaroid. Find intensity of transmitted light from the system assuming \[{{I}_{0}}\] be the intensity of polarised light obtained form the first polaroid.

Answer:

(i) Diagram for plane polarised light obtained by scattering. 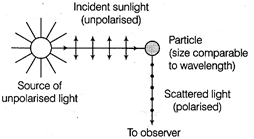Figure shows the unpolarised light incident on the particle. The dots stand for polarisation perpendicular to the plane of the figure. Here, the light wave scattered by molecules is represented by dots. A point is to be noted here that under the influence of electric field of incident (light) wave, the electrons within the particle (on which light is incident) acquire component of motions in two directions (along the plane of figure). Clearly, charges accelerating parallel to the double arrows do not radiate energy towards the observer. Since, their acceleration has no transverse component (that is why the wave scattered by molecules is represented by dots). The wave (light) is polarised perpendicular to the plane of the figure. It also explains the polarisation of scattered light from the sky. (ii) As two polaroids are in crossed position and the third Polaroid is inserted between them which is making an angle of \[30{}^\circ \] with the axis of cross polaroid. Clearly, the third polaroid is making an angle of \[60{}^\circ \] with the axis of first polaroid and 30° with the other Polaroid. If \[{{I}_{0}}\] is the intensity of light obtained from first polaroid, then new intensity of light obtained from the third (middle) polaroid would be \[I'={{I}_{0}}{{\cos }^{2}}60{}^\circ ={{I}_{0}}{{(1/2)}^{2}}\Rightarrow I'={{I}_{0}}/4\] Now, intensity of light obtained from polaroid situated at the end. \[I''=I'{{\cos }^{2}}30{}^\circ =\frac{{{I}_{0}}}{4}{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}=\frac{3{{I}_{0}}}{16}\]