question_answer

Show that the shortest wavelength lines in Lyman, Balmer and Paschen series have their wavelengths in the ratio 1 : 4 : 9.

Or

Prove that the radius of the nth Bohr orbit of an atom is directly proportional to \[{{n}^{2}},\] where n is principal quantum number.

Answer:

For shortest wavelength of Lyman series \[{{n}_{1}}=1,\] \[{{n}_{2}}=\infty \] \[\frac{1}{{{\lambda }_{LS}}}=R\left[ \frac{1}{{{1}^{2}}}-\frac{1}{{{\infty }^{2}}} \right]=R;{{\lambda }_{LS}}=\frac{1}{R}\] For shortest wavelength of Balmer series.             \[{{n}_{1}}=2,\] \[{{n}_{2}}=\infty \] \[\frac{1}{{{\lambda }_{BS}}}=R\left[ \frac{1}{{{2}^{2}}}-\frac{1}{{{\infty }^{2}}} \right]=\frac{R}{4};\,\,{{\lambda }_{BS}}=\frac{4}{R}\] For shortest wavelength of Paschen series             \[{{n}_{1}}=3,\] \[{{n}_{2}}=\infty \] \[\frac{1}{{{\lambda }_{PS}}}=R\left[ \frac{1}{{{3}^{2}}}-\frac{1}{{{\infty }^{2}}} \right]=\frac{R}{9};{{\lambda }_{PS}}=\frac{9}{R}\] Hence, \[{{\lambda }_{LS}}:{{\lambda }_{BS}}:{{\lambda }_{PS}}=1:4:9\] Or Radius of nth Bohr's orbit To keep the electron in its orbit, the centripetal force on the electron must be equal to the electrostatic attraction. Therefore, \[\frac{m{{v}^{2}}}{r}=\frac{k'Z{{e}^{2}}}{{{r}^{2}}}\] where ,  \[k'=\frac{1}{4\pi {{\varepsilon }_{0}}}\] \[\Rightarrow \]   \[r=k'Z{{e}^{2}}/m{{v}^{2}}\]                                   ?(i) 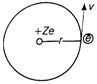where, m is the mass of the electron and v its speed in an orbit of radius r. Bohr's quantisation condition for angular momentum is, \[mvr=\frac{nh}{2\pi }\] \[\Rightarrow r=\frac{nh}{2\pi mv}\]                    ?(ii) From Eqs. (i) and (ii), we get             \[\frac{k'Z{{e}^{2}}}{m{{v}^{2}}}=\frac{nh}{2\pi mv}\Rightarrow v=\frac{2\pi k'Z{{e}^{2}}}{nh}\] Putting this value of v in Eq. (ii), we get \[r=\frac{nh}{2\pi m}\frac{nh}{2\pi k'Z{{e}^{2}}}=\frac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}mk'Z{{e}^{2}}}\] or \[r\propto {{n}^{2}}\] Hence proved.