question_answer

Answer the following questions.

(i) You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce real images under such circumstances? Explain.

(ii) A virtual image, we always say, cannot be caught on a screen.

Yet when we see a virtual image, we are obviously bringing it on to the 'screen' (i.e. the retina) of our eye. Is there a contradiction?

(iii) A diver under water, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?

(iv) Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?

(v) The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?

Or

(i) State Huygens' principle. Using this principle, draw a diagram to show how a plane wavefront incident at the interference of the two media gets refracted when it propagates from a rarer to a denser medium. Hence, verify Snell's law of refraction.

(ii) Is the frequency of reflected and refracted light same as the frequency of incident light?

Answer:

Yes, plane and convex mirrors produces the real image, if the rays incident on the plane or convex mirror are converging to a point behind the mirror. Because they are reflected to a point on a screen in front of the mirror. In other words, a plane or convex mirror can produce a real image of a virtual object. (ii) No, there is no contradiction because virtual image formed by the spherical mirror acts as virtual object for eye lens. Our eye lens is convergent and it forms a real image of virtual object on retina. (iii) As, the fisherman is in air, the rays of light travels from rarer to denser medium, they bend towards the normal. So, the fisherman appears taller. 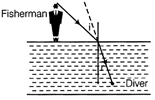(iv) Yes, the apparent depth decreases, further, when water tank is viewed obliquely as compared to the depth when seen near normally (v) Refractive index of diamond \[{{\mu }_{diamond}}>\] Refractive index of glass\[{{\mu }_{glass.}}\] Refractive index, \[\mu =\frac{1}{\sin {{i}_{c}}},\] where \[{{i}_{c}}\] is the critical angle. As, the refractive index of diamond is more than the refractive index of glass, so the value of critical angle for glass is more than diamond. A diamond cutter, cuts the diamond at large range of angle of incidence to ensure that light entering in the diamond suffers from multiple total external reflections. This gives the sparkling effect to diamond. Or (i) Huygens' Principle Each point on the primary wavefront acts as a source of secondary wavelets, sending out disturbance in all directions in a similar manner as the original source of light does. The new position of the wavefront at any instant (called secondary wavefront) is the envelope of the secondary wavelets at that instant. Refraction on the Basis of Wave Theory 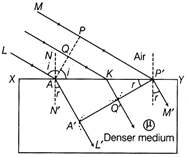Consider any point Q on the incident wavefront. Suppose, when disturbance from point P on incident wavefront PA reaches point P' on the refracted wavefront, the disturbance from point Q reaches Q? on the refracted wavefront P?A? Since P'A' represents the refracted wavefront, the time taken by light to travel from a point on incident wavefront to the corresponding point on refracted wavefront should always be the same. Now, time taken by light to go from Q to Q? will bet \[=\frac{QK}{c}+\frac{KQ'}{v}\]                                   ?(i) Here,     c = speed of light and       v = speed of light in denser medium. In right angled \[\Delta \,AQK,\] \[\angle QAK=i\] \[\therefore \]      \[QK=AK\,sin\,i\]                                    ...(ii) In right angled \[\Delta \,P'Q'K,\] \[\angle Q'P'K=r\] and \[KQ'=KP'sinr\]                   ?(iii) Substituting Eqs. (ii) and (iii) in Eq. (i),             \[t=\frac{AK\sin i}{c}+\frac{KP'\sin r}{v}\] or         \[t=\frac{AK\sin i}{c}+\frac{(AP'-AK)\sin r}{v}\]                                     \[[\because \,\,KP'=AP'-AK]\] or         \[t=\frac{AP'}{v}\sin r+AK\left( \frac{\operatorname{sini}}{c}-\frac{\sin r}{v} \right)\]         ?(iv) The rays from different points on the incident wavefront will take the same time to reach the corresponding points on the refracted wavefront, i.e. r is given by Eq. (iv) is independent of AK.. It will happen so, if \[\frac{\sin i}{c}-\frac{\sin r}{v}=0\] \[\Rightarrow \]   \[\frac{\sin i}{\sin r}=\frac{c}{v}\Rightarrow \mu =\frac{\sin i}{\sin r}\] This is the Snell's law for refraction of light. (ii) The frequency of reflected and refracted light remains same as the frequency of incident light because frequency only depends on the source of light.