question_answer

 

Given figure shows a charge array known as an electric quadruple. For a point on the axis of the quadruple, obtain the dependence of potential on r for \[r/a>>1\] and contrast your results with that due to an electric dipole and an electric monopole (i.e. a single charge).

Electric quadruple

OR

(i) Describe schematically the equipotential surfaces corresponding to

(a) a constant electric field in the Z-direction,

(b) a field that uniformly increases in magnitude but remains in a constant (say Z) direction and

(c) a single positive charge at the origin.

(ii) What is the effect on the interference fringes to a Young's double slit experiment when

(a) the separation between the two slits is increased?

(b) the width of the source-slit is decreased?

           

Answer:

Given, AC = 2a, BP = r, \[AP=r+a\] and \[PC=r-a\] Let potential at P is V. V = Potential at P due to A + Potential at P due to B + Potential at P due to C \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\left[ \frac{q}{AP}-\frac{2q}{BP}+\frac{q}{CP} \right]\] \[=\frac{1}{4\pi {{\varepsilon }_{0}}}\cdot q\left[ \frac{1}{r+a}-\frac{2}{r}+\frac{1}{r-a} \right]\] \[=\frac{q}{4\pi {{\varepsilon }_{0}}}\left[ \frac{r(r-a)-2(r+a)(r-a)+r(r+a)}{r(r+a)(r-a)} \right]\] \[=\frac{q}{4\pi {{\varepsilon }_{0}}}\left[ \frac{{{r}^{2}}-ra-2{{r}^{2}}+2{{a}^{2}}+{{r}^{2}}+ra}{r({{r}^{2}}-{{a}^{2}})} \right]\] \[=\frac{q.2{{a}^{2}}}{4\pi {{\varepsilon }_{0}}r({{r}^{2}}+{{a}^{2}})}=\frac{q.2{{a}^{2}}}{4\pi {{\varepsilon }_{0}}\cdot r\cdot {{r}^{2}}\left( 1-\frac{{{a}^{2}}}{{{r}^{2}}} \right)}\] According to the question, \[If\frac{r}{a}>>1\]  or \[a<<r\] \[\therefore \]      \[V\approx \frac{q\cdot 2{{a}^{2}}}{4\pi {{\varepsilon }_{0}}\cdot {{r}^{3}}}\Rightarrow V\propto \frac{1}{{{r}^{3}}}\] As we know that electric potential at a point on axial line due to an electric dipole, \[V\propto \frac{1}{{{r}^{3}}}.\] In case of electric monopole         \[V\propto \frac{1}{r}.\] Then, we conclude that for larger r, the electric potential due to a quadruple is inversely proportional to the cube of the distance r, while due to an electric dipole it is inversely proportional to the square of r and inversely proportional to the distance r for a monopole. Or (i) (a) As, the constant electric field in the z-axis direction, the equipotential surfaces are normal to the field, i.e. in XY-plane. The equipotential surfaces are equidistant from each other. 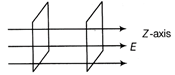Electric field in Z-direction (b) As, the electric field increases in the direction of Z-axis, the equipotential surface is normal to Z-axis i.e. in XY-plane and they become closer and closer as the field increases. 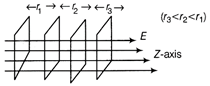(c) As, a single positive charge placed at origin, the equipotential surfaces are concentric spheres with origin at centre. 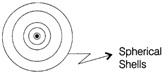(ii) (a) From the fringe width expression,\[\beta =\frac{\lambda D}{d}\] With the increase in separation between two slits, the fringe width \[\beta \] decreases (b) For interference fringes to be seen, \[\frac{s}{S}<\frac{\lambda }{d}\] Condition should be satisfied where,   s = size of the source, S = distance of the source from the plane of two slits. As, the source slit width decreases fringe pattern gets more sharp.