question_answer

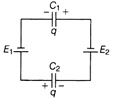
Determine the potential difference across the plates of the capacitor C i of the network shown in the figure. (Assume, \[{{E}_{2}}>{{E}_{1}}\]).

OR

A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor, How much electrostatic energy is lost in the process?

  

Answer:

Effective emf in the circuit, \[E={{E}_{2}}-{{E}_{1}}\] The net capacitance in the circuit, \[C=\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}\] Charge on each capacitor, \[q=C\cdot E=\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}({{E}_{2}}-{{E}_{1}})\] The potential difference across the plates of \[{{C}_{1}},\] \[V=\frac{q}{{{C}_{1}}}=\frac{{{C}_{1}}{{C}_{2}}}{({{C}_{1}}+{{C}_{2}})}\frac{({{E}_{2}}-{{E}_{1}})}{{{C}_{1}}}\]             \[=\frac{{{C}_{2}}({{E}_{2}}-{{E}_{1}})}{({{C}_{1}}+{{C}_{2}})}\] Or Given,   \[{{C}_{1}}={{C}_{2}}=600\times {{10}^{-12}}F\]             \[{{V}_{1}}=200V,\]     \[{{V}_{2}}=0\] \[\therefore \] Loss of energy,\[\Delta U=\frac{{{C}_{1}}{{C}_{2}}}{2({{C}_{1}}+{{C}_{2}})}{{({{V}_{1}}-{{V}_{2}})}^{2}}\]             \[=\frac{600\times {{10}^{-12}}\times 600\times {{10}^{-12}}}{2(600+600)\times {{10}^{-12}}}{{(200-0)}^{2}}\]             \[=\frac{36\times {{10}^{-8}}}{2400}\times 4\times {{10}^{4}}=6\times {{10}^{-6}}J\]